ಸಮಾವೇಶ

ಪರಿವರ್ತನೆ ಎನ್ನುವುದು ಎಫ್ (revers) ನ ವ್ಯತಿರಿಕ್ತ ಕ್ರಿಯೆ ಜಿ (ಟಿ-) ನೊಂದಿಗೆ ಪರಸ್ಪರ ಸಂಬಂಧ ಹೊಂದಿದೆ.

ಕನ್ವಲ್ಯೂಷನ್ ಆಪರೇಟರ್ ನಕ್ಷತ್ರ ಚಿಹ್ನೆ * .

ನಿರಂತರ ಪರಿವರ್ತನೆ
ಡಿಸ್ಕ್ರೀಟ್ ಕನ್ವಲ್ಯೂಷನ್
2 ಡಿ ಡಿಸ್ಕ್ರೀಟ್ ಕನ್ವಲ್ಯೂಷನ್
ದೃ conv ೀಕರಣದೊಂದಿಗೆ ಫಿಲ್ಟರ್ ಅನುಷ್ಠಾನ
ಪರಿವರ್ತನೆ ಪ್ರಮೇಯ

ನಿರಂತರ ಪರಿವರ್ತನೆ

ಎಫ್ (ಟಿ) ಮತ್ತು ಜಿ (ಟಿ) ನ ಕನ್ವಿಲೇಶನ್ ಎಫ್ (τ) ಬಾರಿ ಎಫ್ (ಟಿ-τ) ನ ಅವಿಭಾಜ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:

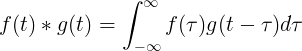
$f (t) * g (t) = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) d \ tau$

ಡಿಸ್ಕ್ರೀಟ್ ಕನ್ವಲ್ಯೂಷನ್

2 ಪ್ರತ್ಯೇಕ ಕಾರ್ಯಗಳ ಪರಿವರ್ತನೆಯನ್ನು ಹೀಗೆ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ:

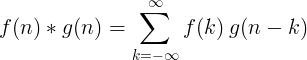
$f (n) * g (n) = \ sum_ {k = - \ infty} ^ {\ infty} f (k) \: g (nk)$

2 ಡಿ ಡಿಸ್ಕ್ರೀಟ್ ಕನ್ವಲ್ಯೂಷನ್

ಇಮೇಜ್ ಪ್ರಕ್ರಿಯೆಗೆ 2 ಆಯಾಮದ ಡಿಸ್ಕ್ರೀಟ್ ಕನ್ವಿಲೇಶನ್ ಅನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಬಳಸಲಾಗುತ್ತದೆ.

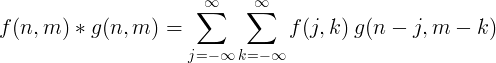
$f (n, m) * g (n, m) = \ sum_ {j = - \ infty} ^ {\ infty} \ sum_ {k = - \ infty} ^ {\ infty} f (j, k) \: g (nj, mk)$

ದೃ conv ೀಕರಣದೊಂದಿಗೆ ಫಿಲ್ಟರ್ ಅನುಷ್ಠಾನ

(ಟ್ಪುಟ್ ಸಿಗ್ನಲ್ ವೈ (ಎನ್) ಪಡೆಯಲು ನಾವು ಪ್ರಚೋದನೆಯ ಪ್ರತಿಕ್ರಿಯೆಯ ಎಚ್ (ಎನ್) ನೊಂದಿಗೆ ಪರಿವರ್ತನೆಯ ಮೂಲಕ ಡಿಸ್ಕ್ರೀಟ್ ಇನ್ಪುಟ್ ಸಿಗ್ನಲ್ ಎಕ್ಸ್ (ಎನ್) ಅನ್ನು ಫಿಲ್ಟರ್ ಮಾಡಬಹುದು.

y ( n ) = x ( n ) * h ( n )

ಪರಿವರ್ತನೆ ಪ್ರಮೇಯ

2 ಕಾರ್ಯಗಳ ಗುಣಾಕಾರದ ಫೋರಿಯರ್ ರೂಪಾಂತರವು ಪ್ರತಿ ಕಾರ್ಯದ ಫೋರಿಯರ್ ರೂಪಾಂತರಗಳ ದೃ olution ೀಕರಣಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:

ℱ { f ⋅ g } = ℱ { f } * ℱ { g }

2 ಕಾರ್ಯಗಳ ಪರಿವರ್ತನೆಯ ಫೋರಿಯರ್ ರೂಪಾಂತರವು ಪ್ರತಿ ಕಾರ್ಯದ ಫೋರಿಯರ್ ರೂಪಾಂತರಗಳ ಗುಣಾಕಾರಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:

ℱ { f * g } = ℱ { f } ⋅ g { g }

ನಿರಂತರ ಫೋರಿಯರ್ ರೂಪಾಂತರಕ್ಕಾಗಿ ಪರಿವರ್ತನೆ ಪ್ರಮೇಯ

ℱ { ಎಫ್ ( ಟಿ ) ⋅ ಗ್ರಾಂ ( ಟಿ )} = ℱ { ಎಫ್ ( ಟಿ )} * ℱ { ಗ್ರಾಂ ( ಟಿ )} = ಎಫ್ ( ω ) * ಜಿ ( ω )

ℱ { ಎಫ್ ( ಟಿ ) * ಗ್ರಾಂ ( ಟಿ )} = ℱ { ಎಫ್ ( ಟಿ )} ⋅ ℱ { ಗ್ರಾಂ ( ಟಿ )} = ಎಫ್ ( ω ) ⋅ ಜಿ ( ω )

ಡಿಸ್ಕ್ರೀಟ್ ಫೋರಿಯರ್ ರೂಪಾಂತರದ ಪರಿವರ್ತನೆ ಪ್ರಮೇಯ

ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )

ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) G ( k )

ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರದ ಪರಿವರ್ತನೆ ಪ್ರಮೇಯ

ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( ಗಳು ) ⋅ G ( ಗಳು )