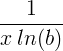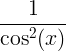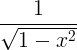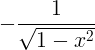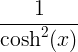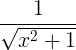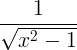ವ್ಯುತ್ಪನ್ನ ನಿಯಮಗಳು

ವ್ಯುತ್ಪನ್ನ ನಿಯಮಗಳು ಮತ್ತು ಕಾನೂನುಗಳು. ಕಾರ್ಯಗಳ ಕೋಷ್ಟಕದ ಉತ್ಪನ್ನಗಳು.

ವ್ಯುತ್ಪನ್ನ ವ್ಯಾಖ್ಯಾನ

ಒಂದು ಕ್ರಿಯೆಯ ವ್ಯುತ್ಪನ್ನವೆಂದರೆ x + Δx ಮತ್ತು x pointsx ನೊಂದಿಗೆ x ()x) ಬಿಂದುಗಳಲ್ಲಿನ ಕಾರ್ಯ ಮೌಲ್ಯ f (x) ನ ವ್ಯತ್ಯಾಸದ ಅನುಪಾತ, Δx ಅನಂತವಾಗಿ ಚಿಕ್ಕದಾಗಿದ್ದಾಗ. ವ್ಯುತ್ಪನ್ನವೆಂದರೆ ಪಾಯಿಂಟ್ x ನಲ್ಲಿ ಸ್ಪರ್ಶಕ ರೇಖೆಯ ಕಾರ್ಯ ಇಳಿಜಾರು ಅಥವಾ ಇಳಿಜಾರು.

 

f '(x) = \ lim _ {\ Delta x \ to 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}

ಎರಡನೇ ಉತ್ಪನ್ನ

ಎರಡನೇ ಉತ್ಪನ್ನವನ್ನು ಇವರಿಂದ ನೀಡಲಾಗಿದೆ:

ಅಥವಾ ಮೊದಲ ವ್ಯುತ್ಪನ್ನವನ್ನು ಪಡೆದುಕೊಳ್ಳಿ:

f '' (x) = (f '(x))'

N ನೇ ಉತ್ಪನ್ನ

ಎನ್ ನೇ ಉತ್ಪನ್ನ f (x), N ಬಾರಿ ವ್ಯುತ್ಪನ್ನಗೊಂಡ ಮೂಲಕ ಕಂಡುಹಿಡಿಯಲಾಗುತ್ತದೆ.

ಎನ್ ನೇ ಜನ್ಯ ಸಂಖ್ಯೆ (n -1) ಉತ್ಪನ್ನ ನಿಷ್ಪನ್ನವಾಗಿದೆ ಸಮ:

f ( n ) ( x ) = [ f ( n -1) ( x )] '

ಉದಾಹರಣೆ:

ನ ನಾಲ್ಕನೇ ಉತ್ಪನ್ನವನ್ನು ಹುಡುಕಿ

f ( x ) = 2 x 5

f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x

ಕಾರ್ಯದ ಗ್ರಾಫ್ನಲ್ಲಿ ವ್ಯುತ್ಪನ್ನ

ಒಂದು ಕ್ರಿಯೆಯ ವ್ಯುತ್ಪನ್ನವೆಂದರೆ ಸ್ಪರ್ಶಕ ರೇಖೆಯ ಇಳಿಜಾರು.

ವ್ಯುತ್ಪನ್ನ ನಿಯಮಗಳು

ವ್ಯುತ್ಪನ್ನ ಮೊತ್ತದ ನಿಯಮ

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
ಉತ್ಪನ್ನ ಉತ್ಪನ್ನ ನಿಯಮ

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
ವ್ಯುತ್ಪನ್ನ ಅಂಶ ನಿಯಮ 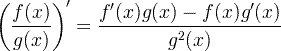\ ಎಡ (\ frac {f (x)} {g (x)} \ ಬಲ) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( X)}
ವ್ಯುತ್ಪನ್ನ ಸರಪಳಿ ನಿಯಮ

f ( g ( x )) '= f' ( g ( x )) g ' ( x )

ವ್ಯುತ್ಪನ್ನ ಮೊತ್ತದ ನಿಯಮ

ಯಾವಾಗ ಒಂದು ಮತ್ತು ಬಿ ಸ್ಥಿರಾಂಕಗಳಾಗಿವೆ.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

ಉದಾಹರಣೆ:

ಇದರ ಉತ್ಪನ್ನವನ್ನು ಹುಡುಕಿ:

3 x 2 + 4 x.

ಮೊತ್ತದ ನಿಯಮದ ಪ್ರಕಾರ:

a = 3, b = 4

f ( x ) = x 2 , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

ಉತ್ಪನ್ನ ಉತ್ಪನ್ನ ನಿಯಮ

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

ವ್ಯುತ್ಪನ್ನ ಅಂಶ ನಿಯಮ

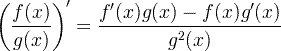
\ ಎಡ (\ frac {f (x)} {g (x)} \ ಬಲ) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( X)}

ವ್ಯುತ್ಪನ್ನ ಸರಪಳಿ ನಿಯಮ

f ( g ( x )) '= f' ( g ( x )) g ' ( x )

ಲಾಗ್ರೇಂಜ್ನ ಸಂಕೇತದೊಂದಿಗೆ ಈ ನಿಯಮವನ್ನು ಚೆನ್ನಾಗಿ ಅರ್ಥಮಾಡಿಕೊಳ್ಳಬಹುದು:

\ frac {df} {dx} = \ frac {df} {dg} d cdot \ frac {dg} x dx}

ಕಾರ್ಯ ರೇಖೀಯ ಅಂದಾಜು

ಸಣ್ಣ Δx ಗಾಗಿ, ನಾವು f (x 0 + Δx) ಗೆ ಅಂದಾಜು ಪಡೆಯಬಹುದು , ನಮಗೆ f (x 0 ) ಮತ್ತು f '(x 0 ) ತಿಳಿದಾಗ :

f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) x

ಕಾರ್ಯಗಳ ಕೋಷ್ಟಕದ ಉತ್ಪನ್ನಗಳು

ಕಾರ್ಯದ ಹೆಸರು ಕಾರ್ಯ ವ್ಯುತ್ಪನ್ನ

f ( x )

 f '( x )
ನಿರಂತರ

const

0

ರೇಖೀಯ

x

1

ಶಕ್ತಿ

x ಎ

ಕೊಡಲಿ a- 1
ಘಾತೀಯ

e x

e x
ಘಾತೀಯ

ಒಂದು x

a x ln a
ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್

ln ( x )

ಲಾಗರಿಥಮ್

ಲಾಗ್ ಬಿ ( ಎಕ್ಸ್ )

ಸೈನ್

ಪಾಪ x

cos x
ಕೊಸೈನ್

cos x

-ಸಿನ್ ಎಕ್ಸ್
ಸ್ಪರ್ಶಕ

ಟ್ಯಾನ್ ಎಕ್ಸ್

ಆರ್ಕ್ಸೈನ್

ಆರ್ಕ್ಸಿನ್ ಎಕ್ಸ್

ಆರ್ಕೊಸೈನ್

ಆರ್ಕೋಸ್ ಎಕ್ಸ್

ಆರ್ಕ್ಟಾಂಜೆಂಟ್

ಆರ್ಕ್ಟಾನ್ ಎಕ್ಸ್
ಹೈಪರ್ಬೋಲಿಕ್ ಸೈನ್

sinh x

cosh x
ಹೈಪರ್ಬೋಲಿಕ್ ಕೊಸೈನ್

cosh x

sinh x
ಹೈಪರ್ಬೋಲಿಕ್ ಸ್ಪರ್ಶಕ

tanh x

ವಿಲೋಮ ಹೈಪರ್ಬೋಲಿಕ್ ಸೈನ್

sinh -1 x

ವಿಲೋಮ ಹೈಪರ್ಬೋಲಿಕ್ ಕೊಸೈನ್

cosh -1 x

ವಿಲೋಮ ಹೈಪರ್ಬೋಲಿಕ್ ಸ್ಪರ್ಶಕ

tanh -1 x

ವ್ಯುತ್ಪನ್ನ ಉದಾಹರಣೆಗಳು

ಉದಾಹರಣೆ # 1

f ( x ) = x 3 +5 x 2 + x +8

f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1

ಉದಾಹರಣೆ # 2

f ( x ) = ಪಾಪ (3 x 2 )

ಸರಣಿ ನಿಯಮವನ್ನು ಅನ್ವಯಿಸುವಾಗ:

f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x

ಎರಡನೇ ಉತ್ಪನ್ನ ಪರೀಕ್ಷೆ

ಯಾವಾಗ ಒಂದು ಕಾರ್ಯ ಮೊದಲ ಉತ್ಪನ್ನವೆಂದು ಪಾಯಿಂಟ್ x ನಲ್ಲಿ ಶೂನ್ಯವಾಗಿರುತ್ತದೆ 0 .

f '( x 0 ) = 0

ನಂತರ x 0 , f '' (x 0 ) ನಲ್ಲಿರುವ ಎರಡನೇ ವ್ಯುತ್ಪನ್ನವು ಆ ಹಂತದ ಪ್ರಕಾರವನ್ನು ಸೂಚಿಸುತ್ತದೆ:

 

f '' ( x 0 )/ 0

 ಸ್ಥಳೀಯ ಕನಿಷ್ಠ

f '' ( x 0 ) <0

 ಸ್ಥಳೀಯ ಗರಿಷ್ಠ

f '' ( x 0 ) = 0

 ನಿರ್ಧರಿಸದ

 

ಸಹ ನೋಡಿ

ಕ್ಯಾಲ್ಕುಲಸ್
ರಾಪಿಡ್ ಟೇಬಲ್‌ಗಳು