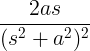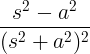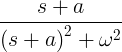ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರ
- ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರ ಕಾರ್ಯ
- ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರ ಟೇಬಲ್
- ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರ ಗುಣಲಕ್ಷಣಗಳು
- ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರ ಉದಾಹರಣೆಗಳು
ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರವು ಶೂನ್ಯದಿಂದ ಅನಂತಕ್ಕೆ ಏಕೀಕರಣದ ಮೂಲಕ ಸಮಯ ಡೊಮೇನ್ ಕಾರ್ಯವನ್ನು ಎಸ್-ಡೊಮೇನ್ ಕಾರ್ಯಕ್ಕೆ ಪರಿವರ್ತಿಸುತ್ತದೆ
ಸಮಯದ ಡೊಮೇನ್ ಕಾರ್ಯದ, e -st ನಿಂದ ಗುಣಿಸಿದಾಗ .
ಡಿಫರೆನ್ಷಿಯಲ್ ಸಮೀಕರಣಗಳು ಮತ್ತು ಅವಿಭಾಜ್ಯಗಳಿಗೆ ತ್ವರಿತವಾಗಿ ಪರಿಹಾರಗಳನ್ನು ಕಂಡುಹಿಡಿಯಲು ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರವನ್ನು ಬಳಸಲಾಗುತ್ತದೆ.
ಸಮಯ ಡೊಮೇನ್ನಲ್ಲಿನ ವ್ಯುತ್ಪನ್ನವನ್ನು s- ಡೊಮೇನ್ನಲ್ಲಿ s ನಿಂದ ಗುಣಿಸಿದಾಗ ಪರಿವರ್ತಿಸಲಾಗುತ್ತದೆ.
ಸಮಯ ಡೊಮೇನ್ನಲ್ಲಿನ ಏಕೀಕರಣವು s- ಡೊಮೇನ್ನಲ್ಲಿ s ನಿಂದ ವಿಭಜನೆಯಾಗಿ ಪರಿವರ್ತನೆಗೊಳ್ಳುತ್ತದೆ.
ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರ ಕಾರ್ಯ
ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರವನ್ನು ಎಲ್ }} ಆಪರೇಟರ್ನೊಂದಿಗೆ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ :
![]()
ವಿಲೋಮ ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರ
ವಿಲೋಮ ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರವನ್ನು ನೇರವಾಗಿ ಲೆಕ್ಕಹಾಕಬಹುದು.
ಸಾಮಾನ್ಯವಾಗಿ ವಿಲೋಮ ರೂಪಾಂತರವನ್ನು ರೂಪಾಂತರ ಕೋಷ್ಟಕದಿಂದ ನೀಡಲಾಗುತ್ತದೆ.
ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರ ಟೇಬಲ್
| ಕಾರ್ಯದ ಹೆಸರು | ಸಮಯ ಡೊಮೇನ್ ಕಾರ್ಯ | ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರ |
|---|---|---|
f ( ಟಿ ) |
ಎಫ್ ( ಗಳು ) = ಎಲ್ { ಎಫ್ ( ಟಿ )} |
|
| ನಿರಂತರ | 1 | |
| ರೇಖೀಯ | ಟಿ | |
| ಶಕ್ತಿ | ಟಿ ಎನ್ |
|
| ಶಕ್ತಿ | ಟಿ ಎ |
Γ ( ಒಂದು +1) ⋅ ಗಳು - ( ಒಂದು +1) |
| ಘಾತಾಂಕ | ಇ ನಲ್ಲಿ |
|
| ಸೈನ್ | ಪಾಪದ ನಲ್ಲಿ |
|
| ಕೊಸೈನ್ | ಕಾಸ್ ನಲ್ಲಿ |
|
| ಹೈಪರ್ಬೋಲಿಕ್ ಸೈನ್ | ಮಾನ್ಸಿಂಗ್ ನಲ್ಲಿ |
|
| ಹೈಪರ್ಬೋಲಿಕ್ ಕೊಸೈನ್ | cosh ನಲ್ಲಿ |
|
| ಬೆಳೆಯುತ್ತಿರುವ ಸೈನ್ | ಟಿ ಪಾಪದ ನಲ್ಲಿ |
|
| ಬೆಳೆಯುತ್ತಿರುವ ಕೊಸೈನ್ | ಟಿ ಕಾಸ್ ನಲ್ಲಿ |
|
| ಕೊಳೆಯುತ್ತಿರುವ ಸೈನ್ | e -at ಪಾಪ ωt |
|
| ಕೊಳೆಯುತ್ತಿರುವ ಕೊಸೈನ್ | e -at cos ωt |
|
| ಡೆಲ್ಟಾ ಕಾರ್ಯ | δ ( ಟಿ ) |
1 |
| ವಿಳಂಬವಾದ ಡೆಲ್ಟಾ | δ ( ಟಾ ) |
e -as |
ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರ ಗುಣಲಕ್ಷಣಗಳು
| ಆಸ್ತಿಯ ಹೆಸರು | ಸಮಯ ಡೊಮೇನ್ ಕಾರ್ಯ | ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರ | ಕಾಮೆಂಟ್ ಮಾಡಿ |
|---|---|---|---|
f ( ಟಿ ) |
ಎಫ್ ( ಗಳು ) |
||
| ರೇಖೀಯತೆ | af ( t ) + bg ( t ) | aF ( ಗಳು ) + bG ( ಗಳು ) | a , b ಸ್ಥಿರವಾಗಿರುತ್ತದೆ |
| ಸ್ಕೇಲ್ ಬದಲಾವಣೆ | f ( ನಲ್ಲಿ ) | |
a / 0 |
| ಶಿಫ್ಟ್ | e -at f ( t ) | ಎಫ್ ( ರು + ಎ ) | |
| ವಿಳಂಬ | f ( ta ) | ಇ - ಮಾಹಿತಿ ಎಫ್ ( ಗಳು ) | |
| ವ್ಯುತ್ಪತ್ತಿ | |
sF ( ಗಳು ) - f (0) | |
| ಎನ್-ನೇ ವ್ಯುತ್ಪತ್ತಿ | |
s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0) | |
| ಶಕ್ತಿ | t n f ( t ) | |
|
| ಏಕೀಕರಣ | |
|
|
| ಪರಸ್ಪರ | |
|
|
| ಸಮಾವೇಶ | f ( t ) * g ( t ) | ಎಫ್ ( ಗಳು ) ⋅ ಜಿ ( ಗಳು ) | * ಕನ್ವಲ್ಯೂಷನ್ ಆಪರೇಟರ್ ಆಗಿದೆ |
| ಆವರ್ತಕ ಕ್ರಿಯೆ | f ( t ) = f ( t + T ) | |
ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರ ಉದಾಹರಣೆಗಳು
ಉದಾಹರಣೆ # 1
ಎಫ್ (ಟಿ) ನ ರೂಪಾಂತರವನ್ನು ಹುಡುಕಿ:
f ( ಟಿ ) = 3 ಟಿ + 2 ಟಿ 2
ಪರಿಹಾರ:
ℒ { t } = 1 / s 2
ℒ { t 2 } = 2 / ಸೆ 3
F ( ಗಳು ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3
ಉದಾಹರಣೆ # 2
ಎಫ್ (ಗಳ) ವಿಲೋಮ ರೂಪಾಂತರವನ್ನು ಹುಡುಕಿ:
ಎಫ್ ( ಗಳು ) = 3 / ( ರು 2 + ಸೆ - 6)
ಪರಿಹಾರ:
ವಿಲೋಮ ರೂಪಾಂತರವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ನಾವು s ಡೊಮೇನ್ ಕಾರ್ಯವನ್ನು ಸರಳ ಸ್ವರೂಪಕ್ಕೆ ಬದಲಾಯಿಸಬೇಕಾಗಿದೆ:
F ( ಗಳು ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)
[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]
a ( s +3) + b ( s -2) = 3
ಎ ಮತ್ತು ಬಿ ಅನ್ನು ಕಂಡುಹಿಡಿಯಲು, ನಾವು 2 ಸಮೀಕರಣಗಳನ್ನು ಪಡೆಯುತ್ತೇವೆ - ಒಂದು ಗುಣಾಂಕಗಳಲ್ಲಿ ಒಂದು ಮತ್ತು ಉಳಿದವು ಎರಡನೆಯದು:
( a + b ) s + 3 a -2 b = 3
a + b = 0, 3 a -2 b = 3
a = 3/5, ಬಿ = -3/5
ಎಫ್ ( ಗಳು ) = 3/5 ( ರು -2) - 3/5 ( ರು +3)
ಘಾತೀಯ ಕಾರ್ಯಕ್ಕಾಗಿ ರೂಪಾಂತರ ಕೋಷ್ಟಕವನ್ನು ಬಳಸುವ ಮೂಲಕ ಈಗ ಎಫ್ (ಗಳನ್ನು) ಸುಲಭವಾಗಿ ಪರಿವರ್ತಿಸಬಹುದು:
f ( ಟಿ ) = (3/5) ಇ 2 ಟಿ - (3/5) ಇ -3 ಟಿ
ಸಹ ನೋಡಿ
ಕ್ಯಾಲ್ಕುಲಸ್
- ಮಿತಿ
- ವ್ಯುತ್ಪನ್ನ
- ಸಮಗ್ರ
- ಸರಣಿ
- ಲ್ಯಾಪ್ಲೇಸ್ ರೂಪಾಂತರ
- ಸಮಾವೇಶ
- ಕ್ಯಾಲ್ಕುಲಸ್ ಚಿಹ್ನೆಗಳು
ರಾಪಿಡ್ ಟೇಬಲ್ಗಳು