ಮೂಲ ಸಂಭವನೀಯತೆ ಸೂತ್ರಗಳು

 

ಸಂಭವನೀಯತೆ ಶ್ರೇಣಿ

0 ≤ ಪಿ ( ಎ ) ≤ 1

ಪೂರಕ ಘಟನೆಗಳ ನಿಯಮ

ಪಿ ( ಎ ಸಿ ) + ಪಿ ( ಎ ) = 1

ಸೇರ್ಪಡೆ ನಿಯಮ

P (A∪B) = P (A) + P (B) - P (A∩B)

ಈವೆಂಟ್‌ಗಳನ್ನು ನಿರಾಕರಿಸು

ಎ ಮತ್ತು ಬಿ ಘಟನೆಗಳು ಇಫ್ಫ್ ಅನ್ನು ಜೋಡಿಸುತ್ತವೆ

P (A∩B) = 0

ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆ

ಪಿ (ಎ | ಬಿ) = ಪಿ (ಎಬಿ) / ಪಿ (ಬಿ)

ಬೇಯ್ಸ್ ಫಾರ್ಮುಲಾ

ಪಿ (ಎ | ಬಿ) = ಪಿ (ಬಿ | ಎ) ⋅ ಪಿ (ಎ) / ಪಿ (ಬಿ)

ಸ್ವತಂತ್ರ ಘಟನೆಗಳು

ಎ ಮತ್ತು ಬಿ ಘಟನೆಗಳು ಸ್ವತಂತ್ರವಾದರೆ

P (A∩B) = P (A) ⋅ P (B)

ಸಂಚಿತ ವಿತರಣಾ ಕಾರ್ಯ

ಎಫ್ ಎಕ್ಸ್ ( ಎಕ್ಸ್ ) = ಪಿ ( ಎಕ್ಸ್ ≤ ಎಕ್ಸ್ )

ಸಂಭವನೀಯತೆ ಸಾಮೂಹಿಕ ಕಾರ್ಯ

ಮೊತ್ತ (i = 1..n, P (X = x (i)) = 1

ಸಂಭವನೀಯತೆ ಸಾಂದ್ರತೆಯ ಕಾರ್ಯ

fX (x) = dFX (x) / dx

FX (x) = ಅವಿಭಾಜ್ಯ (-inf..x, fX (y) * dy)

ಎಫ್ಎಕ್ಸ್ (ಎಕ್ಸ್) = ಮೊತ್ತ (ಕೆ = 1..x, ಪಿ (ಎಕ್ಸ್ = ಕೆ))

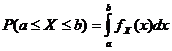
ಪಿ (ಎ <= ಎಕ್ಸ್ <= ಬಿ) = ಅವಿಭಾಜ್ಯ (ಎ..ಬಿ, ಎಫ್ಎಕ್ಸ್ (ಎಕ್ಸ್) * ಡಿಎಕ್ಸ್)

ಅವಿಭಾಜ್ಯ (-inf..inf, fX (x) * dx) = 1

 

ಕೋವಿಯೇರಿಯನ್ಸ್

ಕಾಕ್ಸ್ (ಎಕ್ಸ್, ವೈ) = ಇ (ಎಕ್ಸ್-ಯುಎಕ್ಸ್) (ವೈ-ಯು) = ಇ (ಎಕ್ಸ್‌ವೈ) - ಯುಎಕ್ಸ್ * ಯು

ಪರಸ್ಪರ

corr (X, Y) = Cov (X, Y) / (Std (X) * Std (Y))

 

ಬರ್ನೌಲ್ಲಿ: 0-ವೈಫಲ್ಯ 1-ಯಶಸ್ಸು

ಜ್ಯಾಮಿತೀಯ: 0-ವೈಫಲ್ಯ 1-ಯಶಸ್ಸು

ಹೈಪರ್ಜಿಯೊಮೆಟ್ರಿಕ್: ಕೆ ಯಶಸ್ಸಿನ ವಸ್ತುಗಳನ್ನು ಹೊಂದಿರುವ ಎನ್ ವಸ್ತುಗಳು, ಎನ್ ವಸ್ತುಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ.

 

 

 
 
ಸಂಭವನೀಯತೆ ಮತ್ತು ಅಂಕಿಅಂಶಗಳು
ರಾಪಿಡ್ ಟೇಬಲ್‌ಗಳು