ಸಂಭವನೀಯತೆ ವಿತರಣೆ

ಸಂಭವನೀಯತೆ ಮತ್ತು ಅಂಕಿಅಂಶಗಳ ವಿತರಣೆಯಲ್ಲಿ ಯಾದೃಚ್ variable ಿಕ ವೇರಿಯೇಬಲ್ನ ಒಂದು ಲಕ್ಷಣವಾಗಿದೆ, ಪ್ರತಿ ಮೌಲ್ಯದಲ್ಲಿ ಯಾದೃಚ್ variable ಿಕ ವೇರಿಯೇಬಲ್ನ ಸಂಭವನೀಯತೆಯನ್ನು ವಿವರಿಸುತ್ತದೆ.

ಪ್ರತಿಯೊಂದು ವಿತರಣೆಯು ನಿರ್ದಿಷ್ಟ ಸಂಭವನೀಯತೆ ಸಾಂದ್ರತೆಯ ಕಾರ್ಯ ಮತ್ತು ಸಂಭವನೀಯತೆ ವಿತರಣಾ ಕಾರ್ಯವನ್ನು ಹೊಂದಿದೆ.

ಅನಿರ್ದಿಷ್ಟ ಸಂಖ್ಯೆಯ ಸಂಭವನೀಯತೆ ವಿತರಣೆಗಳಿದ್ದರೂ, ಹಲವಾರು ಸಾಮಾನ್ಯ ವಿತರಣೆಗಳು ಬಳಕೆಯಲ್ಲಿವೆ.

ಸಂಚಿತ ವಿತರಣಾ ಕಾರ್ಯ
ನಿರಂತರ ವಿತರಣಾ ಕೋಷ್ಟಕ
ಪ್ರತ್ಯೇಕ ವಿತರಣಾ ಕೋಷ್ಟಕ

ಸಂಚಿತ ವಿತರಣಾ ಕಾರ್ಯ

ಸಂಭವನೀಯತೆ ವಿತರಣೆಯನ್ನು ಸಂಚಿತ ವಿತರಣಾ ಕಾರ್ಯ ಎಫ್ (ಎಕ್ಸ್) ನಿಂದ ವಿವರಿಸಲಾಗಿದೆ,

ಇದು x ಗಿಂತ ಚಿಕ್ಕದಾದ ಅಥವಾ ಸಮನಾದ ಮೌಲ್ಯವನ್ನು ಪಡೆಯಲು ಯಾದೃಚ್ variable ಿಕ ವೇರಿಯಬಲ್ X ನ ಸಂಭವನೀಯತೆ:

ಎಫ್ ( ಎಕ್ಸ್ ) = ಪಿ ( ಎಕ್ಸ್ ≤ ಎಕ್ಸ್ )

ನಿರಂತರ ವಿತರಣೆ

ಸಂಚಿತ ವಿತರಣಾ ಕಾರ್ಯ ಎಫ್ (ಎಕ್ಸ್) ಅನ್ನು ನಿರಂತರ ಯಾದೃಚ್ variable ಿಕ ವೇರಿಯಬಲ್ ಎಕ್ಸ್‌ನ ಸಂಭವನೀಯತೆ ಸಾಂದ್ರತೆಯ ಕಾರ್ಯ ಎಫ್ (ಯು) ಏಕೀಕರಣದಿಂದ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ.

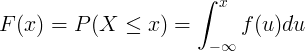
ಪ್ರತ್ಯೇಕ ವಿತರಣೆ

ಸಂಚಿತ ವಿತರಣಾ ಕಾರ್ಯ ಎಫ್ (ಎಕ್ಸ್) ಅನ್ನು ಪ್ರತ್ಯೇಕ ಯಾದೃಚ್ variable ಿಕ ವೇರಿಯಬಲ್ ಎಕ್ಸ್ ನ ಸಂಭವನೀಯತೆ ದ್ರವ್ಯರಾಶಿ ಕ್ರಿಯೆ ಪಿ (ಯು) ನ ಸಂಕಲನದಿಂದ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ.

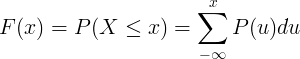
ನಿರಂತರ ವಿತರಣಾ ಕೋಷ್ಟಕ

ನಿರಂತರ ವಿತರಣೆಯು ನಿರಂತರ ಯಾದೃಚ್ variable ಿಕ ವೇರಿಯೇಬಲ್ನ ವಿತರಣೆಯಾಗಿದೆ.

ನಿರಂತರ ವಿತರಣಾ ಉದಾಹರಣೆ

...

ನಿರಂತರ ವಿತರಣಾ ಕೋಷ್ಟಕ

ವಿತರಣೆಯ ಹೆಸರು	ವಿತರಣಾ ಚಿಹ್ನೆ	ಸಂಭವನೀಯತೆ ಸಾಂದ್ರತೆಯ ಕಾರ್ಯ (ಪಿಡಿಎಫ್)	ಸರಾಸರಿ	ವ್ಯತ್ಯಾಸ
		f _X ( x )	μ = ಇ ( ಎಕ್ಸ್ )	σ ² = ಎಲ್ಲಿ ( ಎಕ್ಸ್ )
ಸಾಮಾನ್ಯ / ಗೌಸಿಯನ್	X ~ N (μ, σ ² )	$\ frac {1} {ig ಸಿಗ್ಮಾ \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ ಸಿಗ್ಮಾ ^ 2}}.$	μ	σ ²
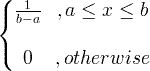ಏಕರೂಪ	ಎಕ್ಸ್ ~ ಯು ( ಎ , ಬಿ )	$\ begin {Bmatrix} \ frac {1} {ba} &, a \ leq x \ leq b \\ & \\ 0 &, ಇಲ್ಲದಿದ್ದರೆ \ end {matrix}$		$\ frac {(ba) ^ 2} {12}$
ಘಾತೀಯ	ಎಕ್ಸ್ ~ ಎಕ್ಸ್ ()	$\ begin {Bmatrix} \ lambda e ^ {- \ lambda x} & x \ geq 0 \\ 0 & x <0 \ end {matrix}$	$\ frac {1} {\ lambda}$	$\ frac {1} {\ lambda ^ 2}$
ಗಾಮಾ	ಎಕ್ಸ್ ~ ಗಾಮಾ ( ಸಿ ,)	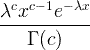$\ frac {\ lambda ^ cx ^ {c-1} e ^ {- \ lambda x}} {amma ಗಾಮಾ (c)}$ x / 0, ಸಿ / 0, λ/ 0	$\ frac {c} {\ lambda}$	$\ frac {c} {\ lambda ^ 2}$
ಚಿ ಚೌಕ	ಎಕ್ಸ್ ~ χ ² ( ಕೆ )	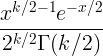$\ frac {x ^ {k / 2-1} e ^ {- x / 2}} {2 ^ {k / 2} amma ಗಾಮಾ (k / 2)}$	ಕೆ	2 ಕೆ
ವಿಶಾರ್ಟ್
ಎಫ್	ಎಕ್ಸ್ ~ ಎಫ್ ( ಕೆ ₁, ಕೆ ₂ )
ಬೀಟಾ
ವೈಬುಲ್
ಲಾಗ್-ಸಾಮಾನ್ಯ	X ~ LN (μ, σ ² )
ರೇಲೀ
ಕೌಚಿ
ಡಿರಿಚ್ಲೆಟ್
ಲ್ಯಾಪ್ಲೇಸ್
ಲೆವಿ
ಅಕ್ಕಿ
ವಿದ್ಯಾರ್ಥಿಗಳ ಟಿ

ಪ್ರತ್ಯೇಕ ವಿತರಣಾ ಕೋಷ್ಟಕ

ಡಿಸ್ಕ್ರೀಟ್ ವಿತರಣೆಯು ಡಿಸ್ಕ್ರೀಟ್ ಯಾದೃಚ್ variable ಿಕ ವೇರಿಯೇಬಲ್ನ ವಿತರಣೆಯಾಗಿದೆ.

ಪ್ರತ್ಯೇಕ ವಿತರಣಾ ಉದಾಹರಣೆ

...

ಪ್ರತ್ಯೇಕ ವಿತರಣಾ ಕೋಷ್ಟಕ

ವಿತರಣೆಯ ಹೆಸರು	ವಿತರಣಾ ಚಿಹ್ನೆ	ಸಂಭವನೀಯ ದ್ರವ್ಯರಾಶಿ ಕ್ರಿಯೆ (pmf)		ಸರಾಸರಿ	ವ್ಯತ್ಯಾಸ
		f _x ( k ) = P ( X = k ) k = 0,1,2, ...		ಇ ( ಎಕ್ಸ್ )	ವರ್ ( ಎಕ್ಸ್ )
ದ್ವಿಪದ	ಎಕ್ಸ್ ~ ಬಿನ್ ( ಎನ್ , ಪು )	$\ ಬೈನೋಮ್ {n} {k} p ^ {k} (1-p) ^ {nk}$		np	np (1- ಪು )
ಪಾಯ್ಸನ್	ಎಕ್ಸ್ ~ ಪಾಯ್ಸನ್ (λ)		λ ≥ 0	λ	λ
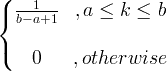ಏಕರೂಪ	ಎಕ್ಸ್ ~ ಯು ( ಎ, ಬಿ )	$\ begin {Bmatrix} \ frac {1} {b-a + 1} &, a \ leq k \ leq b \\ & \\ 0 &, ಇಲ್ಲದಿದ್ದರೆ \ end {matrix}$		$\ frac {a + b} {2}$	$\ frac {(b-a + 1) ^ {2} -1} {12}$
ಜ್ಯಾಮಿತೀಯ	ಎಕ್ಸ್ ~ ಜಿಯೋಮ್ ( ಪು )	$p (1-p) ^ {k}$		$\ frac {1-p} {p}$	$\ frac {1-p} {p ^ 2}$
ಹೈಪರ್-ಜ್ಯಾಮಿತೀಯ	X ~ HG ( N , K , n )		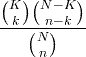ಎನ್ = 0,1,2, ... ಕೆ = 0,1, .., ಎನ್ n = 0,1, ..., ಎನ್	$\ frac {nK} {N}$	$\ frac {nK (NK) (Nn)} {N ^ 2 (N-1)}$
ಬರ್ನೌಲ್ಲಿ	ಎಕ್ಸ್ ~ ಬರ್ನ್ ( ಪು )	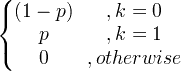$\ begin {Bmatrix} (1-p) &, k = 0 \\ p &, k = 1 \\ 0 &, ಇಲ್ಲದಿದ್ದರೆ \ end {matrix}$		ಪು	p (1- ಪು )

ಸಂಭವನೀಯತೆ ವಿತರಣೆ

ಸಂಚಿತ ವಿತರಣಾ ಕಾರ್ಯ

ನಿರಂತರ ವಿತರಣೆ

ಪ್ರತ್ಯೇಕ ವಿತರಣೆ

ನಿರಂತರ ವಿತರಣಾ ಕೋಷ್ಟಕ

ನಿರಂತರ ವಿತರಣಾ ಉದಾಹರಣೆ

ನಿರಂತರ ವಿತರಣಾ ಕೋಷ್ಟಕ

ಪ್ರತ್ಯೇಕ ವಿತರಣಾ ಕೋಷ್ಟಕ

ಪ್ರತ್ಯೇಕ ವಿತರಣಾ ಉದಾಹರಣೆ

ಪ್ರತ್ಯೇಕ ವಿತರಣಾ ಕೋಷ್ಟಕ

ಸಹ ನೋಡಿ

ಸಂಭವನೀಯತೆ ಮತ್ತು ಅಂಕಿಅಂಶಗಳು

ರಾಪಿಡ್ ಟೇಬಲ್‌ಗಳು