로그 규칙
숫자 의 밑이 b 인 로그 는 숫자 를 얻기 위해 밑 을 올리는 데 필요한 지수 입니다 .
로그 정의
b를 y의 거듭 제곱으로 올릴 때 x는 다음과 같습니다.
b y = x
그러면 x의 기본 b 로그는 y와 같습니다.
로그 b ( x ) = y
예를 들면 다음과 같습니다.
2 4 = 16
그때
로그 2 (16) = 4
지수 함수의 역함수로서의 로그
로그 함수,
y = 로그 b ( x )
지수 함수의 역함수입니다.
X = B Y
따라서 x (x/ 0) 로그의 지수 함수를 계산하면
f ( f -1 ( x )) = b log b ( x ) = x
또는 x의 지수 함수의 로그를 계산하면
f -1 ( f ( x )) = log b ( b x ) = x
자연 로그 (ln)
ln ( x ) = log e ( x )
때 전자 상수 수 있습니다 :
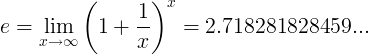
또는
![]()
참조 : 자연 로그
역 로그 계산
역 로그 (또는 역 로그)는 밑이 b를 로그 y로 올려서 계산됩니다.
x = 로그 -1 ( y ) = b y
대수 함수
로그 함수의 기본 형식은 다음과 같습니다.
f ( x ) = 로그 b ( x )
로그 규칙
| 규칙 이름 | 규칙 |
|---|---|
대수 곱 규칙 |
log b ( x ∙ y ) = log b ( x ) + log b ( y ) |
로그 몫 규칙 |
기록 B ( X / Y ) = 로그 B ( X ) - 로그 (B) ( 예를 ) |
로그 거듭 제곱 규칙 |
log b ( x y ) = y ∙ log b ( x ) |
로그베이스 스위치 규칙 |
log b ( c ) = 1 / log c ( b ) |
로그 밑수 변경 규칙 |
log b ( x ) = log c ( x ) / log c ( b ) |
로그의 미분 |
f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b )) |
대수의 적분 |
∫ log b ( x ) dx = x ∙ (log b ( x ) -1 / ln ( b ) ) + C |
음수의 로그 |
log b ( x ) 는 x ≤ 0 일 때 정의되지 않습니다. |
0의 로그 |
log b (0) 은 정의되지 않았습니다. |
1의 로그 |
로그 b (1) = 0 |
밑의 로그 |
로그 b ( b ) = 1 |
무한대의 로그 |
lim log b ( x ) = ∞, x → ∞ 일 때 |
참조 : 로그 규칙
대수 곱 규칙
x와 y의 곱셈의 로그는 x의 로그와 y의 로그의 합입니다.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
예를 들면 :
로그 10 (3 ∙ 7) = 로그 10 (3) + 로그 10 (7)
로그 몫 규칙
x와 y의 나눗셈의 로그는 x의 로그와 y의 로그의 차이입니다.
기록 B ( X / Y ) = 로그 B ( X ) - 로그 (B) ( 예를 )
예를 들면 :
로그 (10) (3 / 7) 로그 = 10 (3) - 기록 (10) (7)
로그 거듭 제곱 규칙
y의 거듭 제곱으로 올린 x의 로그는 x의 로그의 y를 곱한 것입니다.
log b ( x y ) = y ∙ log b ( x )
예를 들면 :
로그 10 (2 8 ) = 8 ∙ 로그 10 (2)
로그베이스 스위치 규칙
c의 기본 b 로그는 b의 기본 c 로그로 나눈 1입니다.
log b ( c ) = 1 / log c ( b )
예를 들면 :
로그 2 (8) = 1 / 로그 8 (2)
로그 밑수 변경 규칙
x의 기본 b 로그는 x의 기본 c 로그를 b의 기본 c 로그로 나눈 값입니다.
log b ( x ) = log c ( x ) / log c ( b )
예를 들어 계산기에서 로그 2 (8)를 계산하려면 밑을 10으로 변경해야합니다.
로그 2 (8) = 로그 10 (8) / 로그 10 (2)
참조 : 로그베이스 변경 규칙
음수의 로그
x <= 0 일 때 x의 기본 b 실수 로그는 x가 음수이거나 0 일 때 정의되지 않습니다.
log b ( x ) 는 x ≤ 0 일 때 정의되지 않습니다.
참조 : 음수의 로그
0의 로그
0의 기본 b 로그는 정의되지 않습니다.
log b (0) 은 정의되지 않았습니다.
x가 0에 가까워 질 때 x의 기본 b 로그 한계는 마이너스 무한대입니다.
![]()
참조 : 로그 0
1의 로그
1의 기본 b 로그는 0입니다.
로그 b (1) = 0
예를 들어, 1의 밑이 2 인 로그는 0입니다.
로그 2 (1) = 0
참조 : 로그
무한대의 로그
x가 무한대에 가까워 질 때 x의 기저 b 로그 한계는 무한대와 같습니다.
lim log b ( x ) = ∞, x → ∞ 일 때
참조 : 무한대의 로그
밑의 로그
b의 기본 b 로그는 다음과 같습니다.
로그 b ( b ) = 1
예를 들어, 2의 밑이 2 인 로그는 1입니다.
로그 2 (2) = 1
로그 미분
언제
f ( x ) = 로그 b ( x )
그런 다음 f (x)의 미분 :
f ' ( x ) = 1 / ( x ln ( b ))
참조 : 로그 미분
대수 적분
x의 로그 적분 :
∫ log b ( x ) dx = x ∙ (log b ( x ) -1 / ln ( b ) ) + C
예를 들면 :
∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) -1 / ln (2) ) + C
대수 근사
로그 2 ( x ) ≈ n + ( x / 2 n -1),
복소 로그
복소수 z의 경우 :
z = re iθ = x + iy
복소 로그는 다음과 같습니다 (n = ...- 2, -1,0,1,2, ...).
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
로그 문제와 답
문제 # 1
x 찾기
로그 2 ( x ) + 로그 2 ( x -3) = 2
해결책:
제품 규칙 사용 :
로그 2 ( x ∙ ( x -3)) = 2
로그 정의에 따라 로그 형식 변경 :
x ∙ ( x -3) = 2 2
또는
x 2 -3 x -4 = 0
2 차 방정식 풀기 :
x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1
음수에 대해 로그가 정의되지 않았으므로 대답은 다음과 같습니다.
x = 4
문제 # 2
x 찾기
로그 3 ( x +2)-로그 3 ( x ) = 2
해결책:
몫 규칙 사용 :
로그 3 (( x +2) / x ) = 2
로그 정의에 따라 로그 형식 변경 :
( x +2) / x = 3 2
또는
x +2 = 9 배
또는
8 x = 2
또는
x = 0.25
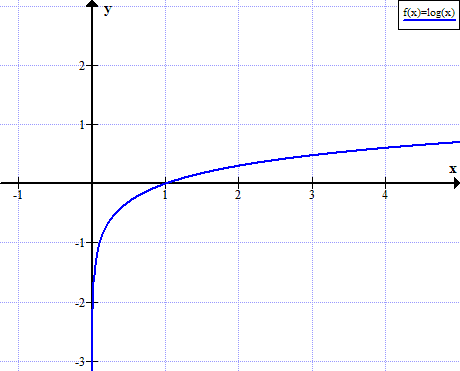
log (x)의 그래프
log (x)는 x의 양수가 아닌 실수 값에 대해 정의되지 않습니다.
로그 테이블
| x | 로그 10 x | 로그 2 x | 로그 e x |
|---|---|---|---|
| 0 | 찾으시는 주소가 없습니다 | 찾으시는 주소가 없습니다 | 찾으시는 주소가 없습니다 |
| 0 + | -∞ | -∞ | -∞ |
| 0.0001 | -4 | -13.287712 | -9.210340 |
| 0.001 | -삼 | -9.965784 | -6.907755 |
| 0.01 | -2 | -6.643856 | -4.605170 |
| 0.1 | -1 | -3.321928 | -2.302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0.301030 | 1 | 0.693147 |
| 3 | 0.477121 | 1.584963 | 1.098612 |
| 4 | 0.602060 | 2 | 1.386294 |
| 5 | 0.698970 | 2.321928 | 1.609438 |
| 6 | 0.778151 | 2.584963 | 1.791759 |
| 7 | 0.845098 | 2.807355 | 1.945910 |
| 8 | 0.903090 | 3 | 2.079442 |
| 9 | 0.954243 | 3.169925 | 2.197225 |
| 10 | 1 | 3.321928 | 2.302585 |
| 20 | 1.301030 | 4.321928 | 2.995732 |
| 30 | 1.477121 | 4.906891 | 3.401197 |
| 40 | 1.602060 | 5.321928 | 3.688879 |
| 50 | 1.698970 | 5.643856 | 3.912023 |
| 60 | 1.778151 | 5.906991 | 4.094345 |
| 70 | 1.845098 | 6.129283 | 4.248495 |
| 80 | 1.903090 | 6.321928 | 4.382027 |
| 90 | 1.954243 | 6.491853 | 4.499810 |
| 100 | 2 | 6.643856 | 4.605170 |
| 200 | 2.301030 | 7.643856 | 5.298317 |
| 300 | 2.477121 | 8.228819 | 5.703782 |
| 400 | 2.602060 | 8.643856 | 5.991465 |
| 500 | 2.698970 | 8.965784 | 6.214608 |
| 600 | 2.778151 | 9.228819 | 6.396930 |
| 700 | 2.845098 | 9.451211 | 6.551080 |
| 800 | 2.903090 | 9.643856 | 6.684612 |
| 900 | 2.954243 | 9.813781 | 6.802395 |
| 1000 | 3 | 9.965784 | 6.907755 |
| 10000 | 4 | 13.287712 | 9.210340 |