e 상수

e 상수 또는 오일러의 수 는 수학 상수입니다. e 상수는 실수이고 무리수입니다.

e = 2.718281828459 ...

e의 정의
e의 속성
밑이 e 로그
지수 함수
오일러의 공식

e의 정의

e 상수는 한계로 정의됩니다.

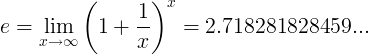
$e = \ lim_ {x \ rightarrow \ infty} \ left (1+ \ frac {1} {x} \ right) ^ x = 2.718281828459 ...$

대체 정의

e 상수는 한계로 정의됩니다.

$e = \ lim_ {x \ rightarrow 0} \ left (1+ \ right x) ^ \ frac {1} {x}$

e 상수는 무한 시리즈로 정의됩니다.

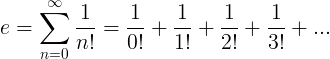
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} { 2!} + \ frac {1} {3!} + ...$

e의 속성

e의 역수

e의 역수는 한계입니다.

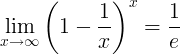
$\ lim_ {x \ rightarrow \ infty} \ left (1- \ frac {1} {x} \ right) ^ x = \ frac {1} {e}$

e의 파생어

지수 함수의 미분은 지수 함수입니다.

( e ^x ) '= e ^x

자연 로그 함수의 미분은 역수 함수입니다.

(log _e x ) '= (ln x )' = 1 / x

e의 적분

지수 함수 e ^x 의 부정적분 은 지수 함수 e ^x 입니다.

∫ e ^x dx = e ^x + c

자연 로그 함수 log _e x 의 부정적분 은 다음과 같습니다.

∫ log _e x dx = ∫ ln x dx = x ln x-x + c

1에서 e까지의 역수 함수 1 / x의 정적분은 1입니다.

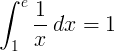
$\ int_ {1} ^ {e} \ frac {1} {x} \ : dx = 1$

밑이 e 로그

숫자 x의 자연 로그는 x의 밑이 e 로그로 정의됩니다.

ln x = 로그 _e x

지수 함수

지수 함수는 다음과 같이 정의됩니다.

f ( x ) = exp ( x ) = e ^x

오일러의 공식

복소수 e ^iθ 는 다음과 같은 동일성을 갖습니다.

e ^iθ = cos ( θ ) + i sin ( θ )

i는 허수 단위 (-1의 제곱근)입니다.

θ는 임의의 실수입니다.