확률 분포
확률 및 통계 분포 는 확률 변수의 특성으로 각 값에서 확률 변수의 확률을 설명합니다.
각 분포에는 특정 확률 밀도 함수와 확률 분포 함수가 있습니다.
확률 분포의 수는 제한되지 않지만 몇 가지 일반적인 분포가 사용됩니다.
누적 분포 함수
확률 분포는 누적 분포 함수 F (x)로 설명됩니다.
이는 x보다 작거나 같은 값을 얻을 확률 변수 X의 확률입니다.
F ( x ) = P ( X ≤ x )
연속 배포
누적 분포 함수 F (x)는 연속 랜덤 변수 X의 확률 밀도 함수 f (u)를 통합하여 계산됩니다.

이산 배포
누적 분포 함수 F (x)는 이산 확률 변수 X의 확률 질량 함수 P (u)의 합으로 계산됩니다.
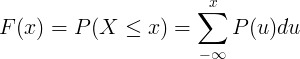
연속 분포 표
연속 분포는 연속 확률 변수의 분포입니다.
연속 배포 예
...
연속 분포 표
| 배포 이름 | 배포 기호 | 확률 밀도 함수 (pdf) | 평균 | 변화 |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| 일반 / 가우스 | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| 제복 | X ~ U ( a , b ) |
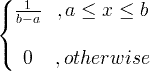 |
|
|
| 지수 | X ~ 특급 (λ) | |
|
|
| 감마 | X ~ 감마 ( c , λ) | 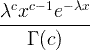 x / 0, c / 0, λ/ 0 |
|
|
| 치 스퀘어 | X ~ χ 2 ( k ) |
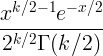 |
k |
2 K |
| Wishart | ||||
| F | X ~ F ( k 1 , k 2 ) |
|||
| 베타 | ||||
| Weibull | ||||
| 로그 정규 | X ~ LN (μ, σ 2 ) |
|||
| 레일리 | ||||
| 코시 | ||||
| Dirichlet | ||||
| 라플라스 | ||||
| 부과 | ||||
| 쌀 | ||||
| 학생의 t |
이산 분포 표
이산 분포는 이산 확률 변수의 분포입니다.
이산 배포 예
...
이산 분포 표
| 배포 이름 | 배포 기호 | 확률 질량 함수 (pmf) | 평균 | 변화 | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| 이항식 | X ~ Bin ( n , p ) |
|
np |
np (1- p ) |
|
| 푸 아송 | X ~ 푸 아송 (λ) |
|
λ ≥ 0 |
λ |
λ |
| 제복 | X ~ U ( a, b ) |
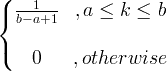 |
|
|
|
| 기하학적 | X ~ 기하학 ( p ) |
|
|
|
|
| 초 기하학적 | X ~ HG ( N , K , n ) |
 |
N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N |
|
|
| 베르누이 | X ~ 베른 ( p ) |
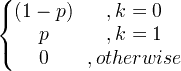 |
p |
p (1- p ) |
|