표준 편차

확률 및 통계에서 랜덤 변수 의 표준 편차 는 평균값에서 랜덤 변수의 평균 거리입니다.

랜덤 변수가 평균값 근처에서 분포되는 방식을 나타냅니다. 작은 표준 편차는 랜덤 변수가 평균값 근처에 분포되어 있음을 나타냅니다. 큰 표준 편차는 랜덤 변수가 평균값에서 멀리 떨어져 있음을 나타냅니다.

표준 편차는 평균값이 μ 인 랜덤 변수 X 분산의 제곱근입니다.

$\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}$

표준 편차의 정의에서 우리는

$\ sigma = std (X) = \ sqrt {E (X ^ 2)-\ mu ^ 2}$

평균값 μ 및 확률 밀도 함수 f (x)를 갖는 연속 랜덤 변수의 경우 :

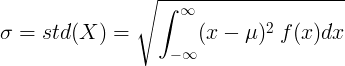
$\ sigma = std (X) = \ sqrt {\ int _ {-\ infty} ^ {\ infty} (x- \ mu) ^ 2 \ : f (x) dx}$

또는

$\ sigma = std (X) = \ sqrt {\ left [\ int _ {-\ infty} ^ {\ infty} x ^ 2 \ : f (x) dx \ right]-\ mu ^ 2}$

평균값이 μ이고 확률 질량 함수가 P (x) 인 이산 형 랜덤 변수 X의 경우 :

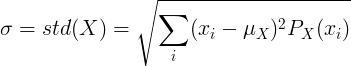
$\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}$

또는

$\ sigma = std (X) = \ sqrt {\ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right]-\ mu ^ 2}$

또한보십시오