Kvadratinė lygtis
Kvadratinė lygtis yra antrosios eilės polinomas su 3 koeficientais - a , b , c .
Kvadratinę lygtį pateikia:
kirvis 2 + bx + c = 0
Kvadratinės lygties sprendimą pateikia 2 skaičiai x 1 ir x 2 .
Kvadratinę lygtį galime pakeisti į:
( x - x 1 ) ( x - x 2 ) = 0
Kvadratinė formulė
Kvadratinės lygties sprendimą pateikia kvadratinė formulė:
![]()
Išraiška kvadratinės šaknies viduje vadinama diskriminuojančia ir žymima Δ:
Δ = b 2 - 4 kint
Kvadratinė formulė su diskriminaciniu žymėjimu:
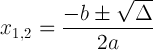
Ši išraiška yra svarbi, nes ji gali mums pasakyti apie sprendimą:
- Kai Δ/ 0, yra 2 tikrosios šaknys x 1 = (- b + √ Δ ) / (2a) ir x 2 = (- b-√ Δ ) / (2a) .
- Kai Δ = 0, yra viena šaknis x 1 = x 2 = -b / (2a) .
- Kai Δ <0, nėra realių šaknų, yra 2 kompleksas šaknys:
x 1 = (- b + i√ -Δ ) / (2a) ir x 2 = (- bi√ -Δ ) / (2a) .
1 problema
3 x 2 +5 x +2 = 0
sprendimas:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
2 problema
3 x 2 -6 x +3 = 0
sprendimas:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
3 problema
x 2 +2 x +5 = 0
sprendimas:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16) )) / 2
Realių sprendimų nėra. Vertės yra sudėtingi skaičiai:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Kvadratinių funkcijų grafikas
Kvadratinė funkcija yra antrosios eilės daugianario funkcija:
f ( x ) = kirvis 2 + bx + c
Kvadratinės lygties sprendiniai yra kvadratinės funkcijos šaknys, ty kvadratinės funkcijos grafiko ir x ašies susikirtimo taškai, kai
f ( x ) = 0
Kai yra 2 grafiko susikirtimo taškai su x ašimi, yra 2 kvadratinės lygties sprendiniai.
Kai yra 1 grafiko susikirtimo taškas su x ašimi, yra 1 kvadratinės lygties sprendimas.
Kai nėra grafo susikirtimo taškų su x ašimi, gauname ne realius sprendimus (arba 2 kompleksinius sprendimus).