Logaritmo taisyklės
Bazė b logaritmas iš skaičių yra eksponentė , kad mes turime pakelti bazę , siekiant gauti skaičių.
- Logaritmo apibrėžimas
- Logaritmo taisyklės
- Logaritmo problemos
- Kompleksinis logaritmas
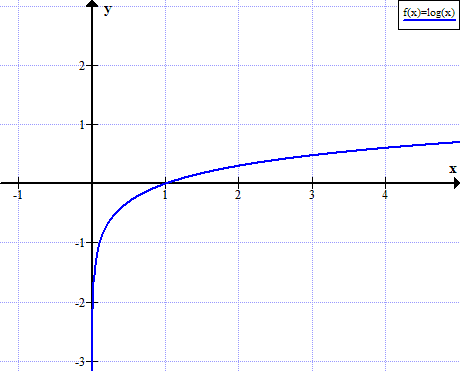
- Žurnalo grafikas (x)
- Logaritmo lentelė
- Logaritmo skaičiuoklė
Logaritmo apibrėžimas
Kai b pakeltas iki y galios, yra lygus x:
b y = x
Tada x bazinis b logaritmas yra lygus y:
log b ( x ) = y
Pavyzdžiui, kai:
2 4 = 16
Tada
log 2 (16) = 4
Logaritmas kaip atvirkštinė eksponentinės funkcijos funkcija
Logaritminė funkcija,
y = log b ( x )
yra atvirkštinė eksponentinės funkcijos funkcija,
x = b y
Taigi, jei apskaičiuosime x (x/ 0) logaritmo eksponentinę funkciją,
f ( f -1 ( x )) = b log b ( x ) = x
Arba, jei apskaičiuosime x eksponentinės funkcijos logaritmą,
f -1 ( f ( x )) = log b ( b x ) = x
Natūralus logaritmas (ln)
Natūralusis logaritmas yra pagrindo e logaritmas:
ln ( x ) = log e ( x )
Kai e konstanta yra skaičius:
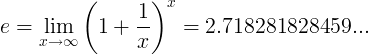
arba
![]()
Žr .: Natūralusis logaritmas
Atvirkštinio logaritmo skaičiavimas
Atvirkštinis logaritmas (arba antilogaritmas) apskaičiuojamas pakeliant pagrindą b į logaritmą y:
x = log -1 ( y ) = b y
Logaritminė funkcija
Logaritminė funkcija turi pagrindinę formą:
f ( x ) = log b ( x )
Logaritmo taisyklės
| Taisyklės pavadinimas | Taisyklė |
|---|---|
Logaritmo produkto taisyklė |
log b ( x ∙ y ) = log b ( x ) + log b ( y ) |
Logaritmo koeficiento taisyklė |
log b ( x / y ) = log b ( x ) - log b ( y ) |
Logaritmo galios taisyklė |
log b ( x y ) = y ∙ log b ( x ) |
Logaritmo pagrindo jungiklio taisyklė |
log b ( c ) = 1 / log c ( b ) |
Logaritmo pagrindo keitimo taisyklė |
log b ( x ) = log c ( x ) / log c ( b ) |
Logaritmo vedinys |
f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b )) |
Logaritmo integralas |
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C |
Neigiamo skaičiaus logaritmas |
log b ( x ) nėra apibrėžtas, kai x ≤ 0 |
0 logaritmas |
log b (0) nėra apibrėžtas |
1 logaritmas |
log b (1) = 0 |
Pagrindo logaritmas |
log b ( b ) = 1 |
Begalybės logaritmas |
lim log b ( x ) = ∞, kai x → ∞ |
Žr .: Logaritmo taisyklės
Logaritmo produkto taisyklė
X ir y daugybos logaritmas yra x ir y logaritmo suma.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Pavyzdžiui:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Logaritmo koeficiento taisyklė
X ir y dalijimosi logaritmas yra x logaritmo ir y logaritmo skirtumas.
log b ( x / y ) = log b ( x ) - log b ( y )
Pavyzdžiui:
prisijungti 10 (3 / 7) = prisijungti 10 (3) - prisijungti 10 (7)
Logaritmo galios taisyklė
X laipsnio, pakelto iki y galios, logaritmas yra y x x logaritmas.
log b ( x y ) = y ∙ log b ( x )
Pavyzdžiui:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Logaritmo pagrindo jungiklio taisyklė
C bazinis b logaritmas yra 1, padalytas iš b pagrindinio c logaritmo.
log b ( c ) = 1 / log c ( b )
Pavyzdžiui:
log 2 (8) = 1 / log 8 (2)
Logaritmo pagrindo keitimo taisyklė
X bazinis b logaritmas yra bazinis c logaritmas x, padalytas iš b pagrindinio c logaritmo.
log b ( x ) = log c ( x ) / log c ( b )
Pvz., Norėdami apskaičiuoti skaičiuoklėje log 2 (8), turime pakeisti bazę į 10:
log 2 (8) = log 10 (8) / log 10 (2)
Žr .: žurnalo bazės keitimo taisyklė
Neigiamo skaičiaus logaritmas
B x realusis logaritmas x, kai x <= 0, nėra apibrėžtas, kai x yra neigiamas arba lygus nuliui:
log b ( x ) nėra apibrėžtas, kai x ≤ 0
Žr .: neigiamo skaičiaus žurnalas
0 logaritmas
B nulinis nulinis logaritmas nėra apibrėžtas:
log b (0) nėra apibrėžtas
Kai x artėja prie nulio, bazinio b logaritmo x riba yra minus begalybė:
![]()
Žiūrėti: nulio žurnalas
1 logaritmas
Vieno bazinis b logaritmas yra nulis:
log b (1) = 0
Pvz., Vieno pagrindo logaritmas yra lygus nuliui:
log 2 (1) = 0
Žiūrėti: vieno žurnalas
Begalybės logaritmas
X bazinio b logaritmo riba, kai x artėja prie begalybės, yra lygi begalybei:
lim log b ( x ) = ∞, kai x → ∞
Žr .: begalybės žurnalas
Pagrindo logaritmas
B pagrindinis b logaritmas yra vienas:
log b ( b ) = 1
Pavyzdžiui, dviejų pagrindinių dviejų logaritmų skaičius yra vienas:
log 2 (2) = 1
Logaritmo darinys
Kada
f ( x ) = log b ( x )
Tada f (x) darinys:
f ' ( x ) = 1 / ( x ln ( b ))
Žr .: žurnalo vedinys
Logaritmo integralas
X logaritmo integralas:
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
Pavyzdžiui:
∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) - 1 / ln (2) ) + C
Logaritmo aproksimacija
log 2 ( x ) ≈ n + ( x / 2 n - 1),
Kompleksinis logaritmas
Kompleksiniam skaičiui z:
z = re iθ = x + iy
Kompleksinis logaritmas bus (n = ...- 2, -1,0,1,2, ...):
Žurnalas z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
Logaritmo problemos ir atsakymai
1 problema
Raskite x
log 2 ( x ) + log 2 ( x -3) = 2
Sprendimas:
Produkto taisyklės naudojimas:
log 2 ( x ∙ ( x -3)) = 2
Logaritmo formos keitimas pagal logaritmo apibrėžimą:
x ∙ ( x -3) = 2 2
Arba
x 2 -3 x -4 = 0
Kvadratinės lygties sprendimas:
x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1
Kadangi logaritmas nėra apibrėžtas neigiamiems skaičiams, atsakymas yra toks:
x = 4
2 problema
Raskite x
log 3 ( x +2) - log 3 ( x ) = 2
Sprendimas:
Naudojant koeficiento taisyklę:
log 3 (( x +2) / x ) = 2
Logaritmo formos keitimas pagal logaritmo apibrėžimą:
( x +2) / x = 3 2
Arba
x +2 = 9 x
Arba
8 x = 2
Arba
x = 0,25
Žurnalo grafikas (x)
log (x) nėra apibrėžtas realioms ne teigiamoms x reikšmėms:
Logaritmų lentelė
| x | rąstas 10 x | žurnalas 2 x | log e x |
|---|---|---|---|
| 0 | neapibrėžtas | neapibrėžtas | neapibrėžtas |
| 0 + | - ∞ | - ∞ | - ∞ |
| 0,0001 | -4 | -13.287712 | -9.210340 |
| 0,001 | -3 | -9,965784 | -6,907755 |
| 0,01 | -2 | -6.643856 | -4.605170 |
| 0.1 | -1 | -3,321928 | -2,302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0,301030 | 1 | 0.693147 |
| 3 | 0.477121 | 1.584963 | 1.098612 |
| 4 | 0,602060 | 2 | 1.386294 |
| 5 | 0.698970 | 2.321928 | 1.609438 |
| 6 | 0.778151 | 2.584963 | 1.791759 |
| 7 | 0.845098 | 2.807355 | 1.945910 |
| 8 | 0,903090 | 3 | 2.079442 |
| 9 | 0,954243 | 3.169925 | 2.197225 |
| 10 | 1 | 3.321928 | 2.302585 |
| 20 | 1.301030 | 4.321928 | 2.995732 |
| 30 | 1.477121 | 4.906891 | 3.401197 |
| 40 | 1.602060 | 5.321928 | 3.688879 |
| 50 | 1.698970 | 5.643856 | 3.912023 |
| 60 | 1.778151 | 5.906991 | 4.094345 |
| 70 | 1.845098 | 6.129283 | 4.248495 |
| 80 | 1.903090 | 6.321928 | 4.382027 |
| 90 | 1.954243 | 6.491853 | 4.499810 |
| 100 | 2 | 6.643856 | 4.605170 |
| 200 | 2.301030 | 7.643856 | 5.298317 |
| 300 | 2.477121 | 8.228819 | 5.703782 |
| 400 | 2.602060 | 8.643856 | 5.991465 |
| 500 | 2.698970 | 8.965784 | 6.214608 |
| 600 | 2.778151 | 9.228819 | 6.396930 |
| 700 | 2.845098 | 9.451211 | 6.551080 |
| 800 | 2.903090 | 9.643856 | 6.684612 |
| 900 | 2.954243 | 9.813781 | 6.802395 |
| 1000 | 3 | 9.965784 | 6.907755 |
| 10000 | 4 | 13.287712 | 9.210340 |
Taip pat žiūrėkite
- Logaritmo taisyklės
- Logaritmo pagrindo pokytis
- Nulio logaritmas
- Vienos logaritmas
- Begalybės logaritmas
- Neigiamo skaičiaus logaritmas
- Logaritmo skaičiuoklė
- Logaritmo grafikas
- Logaritmo lentelė
- Natūralaus logaritmo skaičiuoklė
- Natūralus logaritmas - ln x
- e pastovus
- Decibelai (dB)