Integralus

Integracija yra atvirkštinė darinio operacija.

Funkcijos integralas yra sritis po funkcijos grafiku.

Neapibrėžtas vientisas apibrėžimas

Kada dF (x) / dx = f (x) =/ integralas (f (x) * dx) = F (x) + c

Neapibrėžtos integralios savybės

integralas (f (x) + g (x)) * dx = integralas (f (x) * dx) + integralas (g (x) * dx)

integralas (a * f (x) * dx) = a * integralas (f (x) * dx)

integralas (f (a * x) * dx) = 1 / a * F (a * x) + c

integralas (f (x + b) * dx) = F (x + b) + c

integralas (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

integralas (df (x) / dx * dx) = f (x)

Integracijos kintamojo keitimas

Kadax = g (t) irdx = g '(t) * dt

integralas (f (x) * dx) = integralas (f (g (t)) * g '(t) * dt)

Integravimas dalimis

integralas (f (x) * g '(x) * dx) = f (x) * g (x) - integralas (f' (x) * g (x) * dx)

„Integrals“ lentelė

integralas (f (x) * dx = F (x) + c

integralas (a * dx) = a * x + c

integralas (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, kai a </ - 1

integralas (1 / x * dx) = ln (abs (x)) + c

integralas (e ^ x * dx) = e ^ x + c

integralas (a ^ x * dx) = a ^ x / ln (x) + c

integralas (ln (x) * dx) = x * ln (x) - x + c

integralas (sin (x) * dx) = -cos (x) + c

integralas (cos (x) * dx) = sin (x) + c

integralas (tan (x) * dx) = -ln (abs (cos (x))) + c

integralas (arcsin (x) * dx) = x * arcsin (x) + sqrt (1-x ^ 2) + c

integralas (arccos (x) * dx) = x * arccos (x) - sqrt (1-x ^ 2) + c

integralas (arktanas (x) * dx) = x * arktanas (x) - 1/2 * ln (1 + x ^ 2) + c

integralas (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

integralas (1 / sqrt (a ^ 2-x ^ 2) * dx) = arcsin (x / a) + c

integralas (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

integralas (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

integralas (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * arktanas (x / a) + c

integralas (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

integralas (sinh (x) * dx) = cosh (x) + c

integralas (cosh (x) * dx) = sinh (x) + c

integralas (tanh (x) * dx) = ln (cosh (x)) + c

 

Neapibrėžtas vientisas apibrėžimas

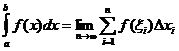
integralas (a..b, f (x) * dx) = lim (n-/ inf, suma (i = 1..n, f (z (i)) * dx (i))) 

Kadax0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

Neapibrėžtas integralinis skaičiavimas

Kada ,

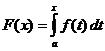 dF (x) / dx = f (x) ir

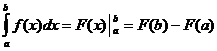
integralas (a..b, f (x) * dx) = F (b) - F (a) 

Neabejotinos integralios savybės

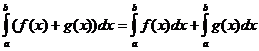
integralas (a..b, (f (x) + g (x)) * dx) = integralas (a..b, f (x) * dx) + integralas (a..b, g (x) * dx )

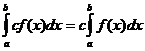
integralas (a..b, c * f (x) * dx) = c * integralas (a..b, f (x) * dx)

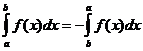
integralas (a..b, f (x) * dx) = - integralas (b..a, f (x) * dx)

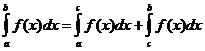
integralas (a..b, f (x) * dx) = integralas (a..c, f (x) * dx) + integralas (c..b, f (x) * dx)

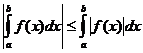
abs (integralas (a..b, f (x) * dx)) <= integralas (a..b, abs (f (x)) * dx)

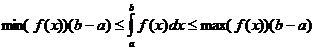min (f (x)) * (ba) <= integralas (a..b, f (x) * dx) <= max (f (x)) * (ba) kadax [a, b] narys

Integracijos kintamojo keitimas

Kadax = g (t) ,dx = g '(t) * dt ,g (alfa) = a ,g (beta) = b

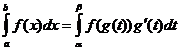
integralas (a..b, f (x) * dx) = integralas (alfa..beta, f (g (t)) * g '(t) * dt)

Integravimas dalimis

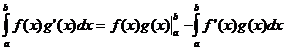
integralas (a..b, f (x) * g '(x) * dx) = integralas (a..b, f (x) * g (x) * dx) - integralas (a..b, f' (x) * g (x) * dx)

Vidutinės vertės teorema

Kai f ( x ) yra ištisinis, yra taškasc yra [a, b] narys taip

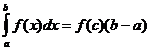
integralas (a..b, f (x) * dx) = f (c) * (ba)  

Trapecinis apibrėžto integralo priartinimas

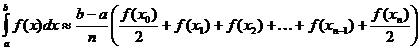
integralas (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

Gama funkcija

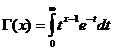
gama (x) = integralas (0..inf, t ^ (x-1) * e ^ (- t) * dt

Gama funkcija konverguoja, kai x/ 0 .

Gama funkcijos ypatybės

G ( x +1) = x G ( x )

G ( n +1) = n ! , kai n ℕ (teigiamas sveikasis skaičius).yra

Beta funkcija

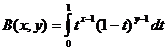
B (x, y) = integralas (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

Beta funkcijos ir gama funkcijos ryšys

B (x, y) = gama (x) * gama (y) / gama (x + y)

 

 

 

KALKULAS
GREITOS LENTELĖS