Pagrindinės tikimybės formulės

 

Tikimybių diapazonas

0 ≤ P ( A ) ≤ 1

Papildomų renginių taisyklė

P ( A C ) + P ( A ) = 1

Papildymo taisyklė

P (A∪B) = P (A) + P (B) - P (A∩B)

Neatskirti įvykiai

A ir B įvykiai yra nesusiję

P (A∩B) = 0

Sąlyginė tikimybė

P (A | B) = P (A∩B) / P (B)

„Bayes“ formulė

P (A | B) = P (B | A) ⋅ P (A) / P (B)

Nepriklausomi renginiai

A ir B įvykiai yra nepriklausomi

P (A∩B) = P (A) ⋅ P (B)

Kaupiamojo paskirstymo funkcija

F X ( x ) = P ( X ≤ x )

Tikimybės masės funkcija

suma (i = 1..n, P (X = x (i)) = 1

Tikimybės tankio funkcija

fX (x) = dFX (x) / dx

FX (x) = integralas (-inf..x, fX (y) * dy)

FX (x) = suma (k = 1..x, P (X = k))

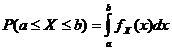
P (a <= X <= b) = integralas (a..b, fX (x) * dx)

integralas (-inf..inf, fX (x) * dx) = 1

 

Kovarsija

Koksas (X, Y) = E (X-ux) (Y-uy) = E (XY) - ux * uy

Koreliacija

corr (X, Y) = Cov (X, Y) / (Standd (X) * Std (Y))

 

Bernoulli: 0 nesėkmės 1 sėkmė

Geometrinė: 0 nesėkmė 1 sėkmė

Hipergeometrinė: N objektai su K sėkmės objektais, n objektai yra paimti.

 

 

 
 
TIKIMYBĖ IR STATISTIKA
GREITOS LENTELĖS