Standartinis nuokrypis

Tikimybėje ir statistikoje atsitiktinio kintamojo standartinis nuokrypis yra vidutinis atsitiktinio kintamojo atstumas nuo vidutinės vertės.

Tai rodo, kaip atsitiktinis kintamasis pasiskirsto netoli vidutinės vertės. Mažas standartinis nuokrypis rodo, kad atsitiktinis kintamasis yra paskirstytas netoli vidutinės vertės. Didelis standartinis nuokrypis rodo, kad atsitiktinis kintamasis yra paskirstytas toli nuo vidutinės vertės.

Standartinio nuokrypio apibrėžimo formulė

Standartinis nuokrypis yra atsitiktinio kintamojo X dispersijos kvadratinė šaknis su vidutine μ verte.

\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

Pagal standartinio nuokrypio apibrėžimą galime gauti

\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Nuolatinio atsitiktinio kintamojo standartinis nuokrypis

Nuolatiniam atsitiktiniam kintamajam, kurio vidutinė vertė μ ir tikimybės tankio funkcija f (x):

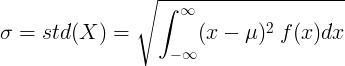
\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

arba

\ sigma = std (X) = \ sqrt {\ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}

Diskretinio atsitiktinio kintamojo standartinis nuokrypis

Diskrečiam atsitiktiniam kintamajam X, kurio vidutinė vertė μ ir tikimybės masės funkcija P (x):

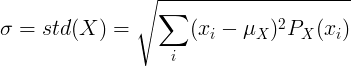
\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

arba

\ sigma = std (X) = \ sqrt {\ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2}

 

Tikimybių pasiskirstymas ►

 

Taip pat žiūrėkite

TIKIMYBĖ IR STATISTIKA
GREITOS LENTELĖS