Nulles numurs (0)
Nulles skaitļa definīcija
Nulle ir skaitlis, ko matemātikā izmanto, lai aprakstītu ne lielumu, ne nulles daudzumu.
Kad uz galda ir 2 āboli un mēs paņemam 2 ābolus, mēs varam teikt, ka uz galda ir nulle ābolu.
Nulles skaitlis nav pozitīvs skaitlis un nav negatīvs skaitlis.
Nulle ir arī viettura cipars citos skaitļos (piemēram: 40 103, 170).
Vai nulle ir skaitlis?
Nulle ir skaitlis. Tas nav pozitīvs vai negatīvs skaitlis.
Nulles cipars
Nulles cipars tiek izmantots kā vietturis, rakstot ciparus.
Piemēram:
204 = 2 × 100 + 0 × 10 + 4 × 1
Nulles skaitļu vēsture
Kas izgudroja nulles skaitli?
Mūsdienu simbols 0 tika izgudrots Indijā 6. gadsimtā, vēlāk to izmantoja persieši un arābi, bet vēlāk Eiropā.
Nulle simbols
Nulles skaitlis tiek apzīmēts ar simbolu 0 .
Arābu ciparu sistēmā tiek izmantots simbols ٠.
Nulles skaitļa īpašības
x apzīmē jebkuru skaitli.
| Darbība | Noteikums | Piemērs |
|---|---|---|
Papildinājums |
x + 0 = x |
3 + 0 = 3 |
Atņemšana |
x - 0 = x |
3 - 0 = 3 |
Reizināšana |
x × 0 = 0 |
5 × 0 = 0 |
Nodaļa |
0 ÷ x = 0 , kad x ≠ 0 |
0 ÷ 5 = 0 |
| x ÷ 0 nav definēts |
5 ÷ 0 nav definēts |
|
Paaugstināšana |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
Sakne |
√ 0 = 0 |
|
Logaritms |
log b (0) nav definēts |
|
| |
||
Faktoriāls |
0! = 1 |
|
Sine |
grēks 0º = 0 |
|
Kosinuss |
cos 0 ° = 1 |
|
Tangents |
iedegums 0º = 0 |
|
Atvasinājums |
0 '= 0 |
|
Neatņemama |
∫ 0 d x = 0 + C |
|
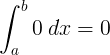 |
Nulles pievienošana
Skaitļa plus nulle pievienošana ir vienāda ar skaitli:
x + 0 = x
Piemēram:
5 + 0 = 5
Nulles atņemšana
Skaitļa atņemšana mīnus nulle ir vienāda ar skaitli:
x - 0 = x
Piemēram:
5 - 0 = 5
Reizināt ar nulli
Skaitļa reizināšana ar nulli ir vienāda ar nulli:
x × 0 = 0
Piemēram:
5 × 0 = 0
Skaitlis dalīts ar nulli
Skaitļa dalījums ar nulli nav definēts:
x ÷ 0 nav definēts
Piemēram:
5 ÷ 0 nav definēts
Nulle dalīta ar skaitli
Nulles dalījums ar skaitli ir nulle:
0 ÷ x = 0
Piemēram:
0 ÷ 5 = 0
Skaitlis līdz nulles jaudai
Par nulli paaugstināta skaitļa jauda ir viena:
x 0 = 1
Piemēram:
5 0 = 1
Nulles logaritms
B nulles bāzes logaritms nav noteikts:
log b (0) nav definēts
Nav skaitļa, ar kuru mēs varētu paaugstināt b b, lai iegūtu nulli.
Tikai x bāzes b logaritma robeža x, kad x saplūst ar nulli, ir mīnus bezgalība:
![]()
Komplekti, kas satur nulli
Nulle ir dabisko skaitļu, veselu skaitļu, reālo skaitļu un komplekso skaitļu kopu elements:
| Iestatīt | Iestatiet dalības apzīmējumu |
|---|---|
| Dabiskie skaitļi (nav negatīvi) | 0 ∈ ℕ 0 |
| Veseli skaitļi | 0 ∈ ℤ |
| Reālie skaitļi | 0 ∈ ℝ |
| Sarežģīti skaitļi | 0 ∈ ℂ |
| Racionālie skaitļi | 0 ∈ ℚ |
Vai nulle ir pāra vai nepāra skaitlis?
Pāra skaitļu kopa ir:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
Nepāra skaitļu kopa ir:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
Nulle ir vesels skaitlis, kas reizināts ar 2:
0 × 2 = 0
Nulle ir pāra skaitļu dalībnieks:
0 ∈ {2 k , k ∈ℤ}
Tātad nulle ir pāra skaitlis, nevis pāra skaitlis.
Vai nulle ir dabisks skaitlis?
Iestatītajiem dabiskajiem skaitļiem ir divas definīcijas.
Nenegatīvu veselu skaitļu kopa:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Pozitīvo veselu skaitļu kopa:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Nulle ir nenegatīvu veselu skaitļu kopas dalībnieks:
0 ∈ ℕ 0
Nulle nav pozitīvo veselu skaitļu kopas dalībniece:
0 ∉ ℕ 1
Vai nulle ir vesels skaitlis?
Veseliem skaitļiem ir trīs definīcijas:
Veselu skaitļu kopa:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Nenegatīvu veselu skaitļu kopa:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Pozitīvo veselu skaitļu kopa:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Nulle ir veselu skaitļu kopas un nenegatīvu veselu skaitļu kopas loceklis:
0 ∈ ℤ
0 ∈ ℕ 0
Nulle nav pozitīvo veselu skaitļu kopas dalībniece:
0 ∉ ℕ 1
Vai nulle ir vesels skaitlis?
Veselu skaitļu kopa:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Nulle ir veselu skaitļu kopas loceklis:
0 ∈ ℤ
Tātad nulle ir vesels skaitlis.
Vai nulle ir racionāls skaitlis?
Racionāls skaitlis ir skaitlis, ko var izteikt kā divu veselu skaitļu dalījumu:
ℚ = { n / m ; n , m ∈ℤ}
Nulli var uzrakstīt kā divu veselu skaitļu dalījumu.
Piemēram:
0 = 0/3
Tātad nulle ir racionāls skaitlis.
Vai nulle ir pozitīvs skaitlis?
Pozitīvs skaitlis tiek definēts kā skaitlis, kas ir lielāks par nulli:
x / 0
Piemēram:
5/ 0
Tā kā nulle nav lielāka par nulli, tas nav pozitīvs skaitlis.
Vai nulle ir galvenais skaitlis?
Skaitlis 0 nav galvenais skaitlis.
Nulle nav pozitīvs skaitlis, un tai ir bezgalīgi daudz dalītāju.
Zemākais primārais skaitlis ir 2.