Varbūtības pamatformulas

 

Varbūtību diapazons

0 ≤ P ( A ) ≤ 1

Papildu pasākumu noteikums

P ( A C ) + P ( A ) = 1

Papildināšanas noteikums

P (A∪B) = P (A) + P (B) - P (A∩B)

Nesakārtoti notikumi

Notikumi A un B nav saistīti

P (A∩B) = 0

Nosacīta varbūtība

P (A | B) = P (A∩B) / P (B)

Bayes formula

P (A | B) = P (B | A) ⋅ P (A) / P (B)

Neatkarīgi notikumi

Notikumi A un B nav neatkarīgi

P (A∩B) = P (A) ⋅ P (B)

Kumulatīvā izplatīšanas funkcija

F X ( x ) = P ( X ≤ x )

Varbūtības masas funkcija

summa (i = 1..n, P (X = x (i)) = 1

Varbūtības blīvuma funkcija

fX (x) = dFX (x) / dx

FX (x) = integrāls (-inf..x, fX (y) * dy)

FX (x) = summa (k = 1..x, P (X = k))

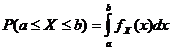
P (a <= X <= b) = integrālis (a..b, fX (x) * dx)

integrālis (-inf..inf, fX (x) * dx) = 1

 

Kovariance

Koksa (X, Y) = E (X-ux) (Y-uy) = E (XY) - ux * uy

Korelācija

corr (X, Y) = Cov (X, Y) / (Std (X) * Std (Y))

 

Bernulli: 0-neveiksme 1-veiksme

Ģeometriskā: 0-neveiksme 1-veiksme

Hipergeometriski: tiek uzņemti N objekti ar K veiksmes objektiem, n objekti.

 

 

 
 
IESPĒJAMĪBA UN STATISTIKA
ĀTRAS TABULAS