Varbūtības sadalījums
Pēc varbūtības un statistikas sadalījums ir nejauša mainīgā raksturojums, apraksta nejaušā mainīgā varbūtību katrā vērtībā.
Katram sadalījumam ir noteikta varbūtības blīvuma funkcija un varbūtības sadalījuma funkcija.
Lai arī varbūtības sadalījumu skaits ir nenoteikts, tiek izmantoti vairāki izplatīti sadalījumi.
Kumulatīvā sadalījuma funkcija
Varbūtības sadalījumu apraksta kumulatīvā sadalījuma funkcija F (x),
kas ir nejaušā mainīgā X varbūtība iegūt vērtību, kas mazāka vai vienāda ar x:
F ( x ) = P ( X ≤ x )
Nepārtraukta izplatīšana
Kumulatīvās sadalījuma funkciju F (x) aprēķina, integrējot nepārtrauktā nejaušā lieluma X varbūtības blīvuma funkciju f (u).
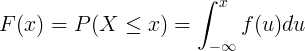
Diskrēts sadalījums
Kumulatīvās sadalījuma funkciju F (x) aprēķina, summējot diskrētā nejaušā lieluma X varbūtības masas funkciju P (u).
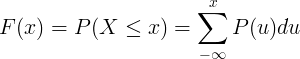
Nepārtraukto sadalījumu tabula
Nepārtraukts sadalījums ir nepārtraukta nejauša mainīgā sadalījums.
Nepārtraukta izplatīšanas piemērs
...
Nepārtraukto sadalījumu tabula
| Izplatīšanas nosaukums | Izplatīšanas simbols | Varbūtības blīvuma funkcija (pdf) | Nozīmē | Dispersija |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| Normāls / gaussāns | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| Vienota | X ~ U ( a , b ) |
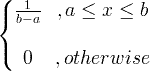 |
|
|
| Eksponenciāls | X ~ exp (λ) | |
|
|
| Gamma | X ~ gamma ( c , λ) | 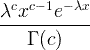 x / 0, c / 0, λ/ 0 |
|
|
| Či laukums | X ~ χ 2 ( k ) |
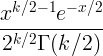 |
k |
2 k |
| Wishart | ||||
| F | X ~ F ( k 1 , k 2 ) |
|||
| Beta | ||||
| Weibull | ||||
| Log-normāli | X ~ LN (μ, σ 2 ) |
|||
| Reilijs | ||||
| Cauchy | ||||
| Dirichlet | ||||
| Laplace | ||||
| Levijs | ||||
| Rīsi | ||||
| Studenta t |
Diskrēto sadalījumu tabula
Diskrētais sadalījums ir diskrēta nejauša mainīgā sadalījums.
Diskrētā sadalījuma piemērs
...
Diskrēto sadalījumu tabula
| Izplatīšanas nosaukums | Izplatīšanas simbols | Varbūtības masas funkcija (pmf) | Nozīmē | Dispersija | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| Binomāls | X ~ tvertne ( n , p ) |
|
np |
np (1- p ) |
|
| Puasons | X ~ Puasons (λ) |
|
λ ≥ 0 |
λ |
λ |
| Vienota | X ~ U ( a, b ) |
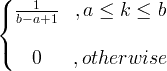 |
|
|
|
| Ģeometriskā | X ~ Geom ( p ) |
|
|
|
|
| Hipergeometriski | X ~ HG ( N , K , n ) |
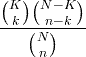 |
N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N |
|
|
| Bernulli | X ~ Berns ( p ) |
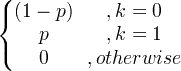 |
p |
p (1- p ) |
|
Skatīt arī
IESPĒJAMĪBA UN STATISTIKA
- Pamata varbūtība
- Gaidīšana
- Dispersija
- Standarta novirze
- Varbūtību sadalījums
- Normāls sadalījums
- Statistikas simboli
ĀTRAS TABULAS