Ecuación cuadrática
La ecuación cuadrática es un polinomio de segundo orden con 3 coeficientes: a , b , c .
La ecuación cuadrática viene dada por:
ax 2 + bx + c = 0
La solución de la ecuación cuadrática viene dada por 2 números x 1 y x 2 .
Podemos cambiar la ecuación cuadrática a la forma de:
( x - x 1 ) ( x - x 2 ) = 0
Fórmula cuadrática
La solución de la ecuación cuadrática viene dada por la fórmula cuadrática:
![]()
La expresión dentro de la raíz cuadrada se llama discriminante y se denota por Δ:
Δ = b 2 - 4 ac
La fórmula cuadrática con notación discriminante:
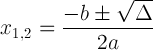
Esta expresión es importante porque nos puede informar sobre la solución:
- Cuando Δ/ 0, hay 2 raíces reales x 1 = (- b + √ Δ ) / (2a) yx 2 = (- b-√ Δ ) / (2a) .
- Cuando Δ = 0, hay una raíz x 1 = x 2 = -b / (2a) .
- Cuando Δ <0, no hay raíces reales, hay 2 raíces complejas:
x 1 = (- b + i√ -Δ ) / (2a) yx 2 = (- bi√ -Δ ) / (2a) .
Problema # 1
3 x 2 +5 x +2 = 0
solución:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 x 3 x 2)) / (2 x 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Problema # 2
3 x 2 -6 x 3 = 0
solución:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 x 3 x 3)) / (2 x 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Problema # 3
x 2 +2 x +5 = 0
solución:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
No hay soluciones reales. Los valores son números complejos:
x 1 = -1 + 2 yo
x 2 = -1 - 2 yo
Gráfico de función cuadrática
La función cuadrática es una función polinomial de segundo orden:
f ( x ) = ax 2 + bx + c
Las soluciones de la ecuación cuadrática son las raíces de la función cuadrática, que son los puntos de intersección de la gráfica de la función cuadrática con el eje x, cuando
f ( x ) = 0
Cuando hay 2 puntos de intersección de la gráfica con el eje x, hay 2 soluciones para la ecuación cuadrática.
Cuando hay 1 punto de intersección de la gráfica con el eje x, hay 1 solución a la ecuación cuadrática.
Cuando no hay puntos de intersección del gráfico con el eje x, no obtenemos soluciones reales (o 2 soluciones complejas).