Reglas de logaritmos
El logaritmo en base b de un número es el exponente que necesitamos para elevar la base para obtener el número.
- Definición de logaritmo
- Reglas de logaritmos
- Problemas de logaritmo
- Logaritmo complejo
- Gráfico de log (x)
- Tabla de logaritmos
- Calculadora de logaritmos
Definición de logaritmo
Cuando b se eleva a la potencia de y es igual a x:
b y = x
Entonces el logaritmo en base b de x es igual ay:
log b ( x ) = y
Por ejemplo cuando:
2 4 = 16
Entonces
log 2 (16) = 4
Logaritmo como función inversa de función exponencial
La función logarítmica,
y = log b ( x )
es la función inversa de la función exponencial,
x = b y
Entonces, si calculamos la función exponencial del logaritmo de x (x/ 0),
f ( f -1 ( x )) = b log b ( x ) = x
O si calculamos el logaritmo de la función exponencial de x,
f -1 ( f ( x )) = log b ( b x ) = x
Logaritmo natural (ln)
El logaritmo natural es un logaritmo en base e:
ln ( x ) = log e ( x )
Cuando e constante es el número:
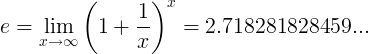
o
![]()
Ver: logaritmo natural
Cálculo del logaritmo inverso
El logaritmo inverso (o antilogaritmo) se calcula elevando la base b al logaritmo y:
x = log -1 ( y ) = b y
Función logarítmica
La función logarítmica tiene la forma básica de:
f ( x ) = log b ( x )
Reglas de logaritmos
| Nombre de la regla | Regla |
|---|---|
Regla de producto de logaritmo |
log b ( x ∙ y ) = log b ( x ) + log b ( y ) |
Regla del cociente de logaritmos |
log b ( x / y ) = log b ( x ) - log b ( y ) |
Regla de potencia de logaritmo |
log b ( x y ) = y ∙ log b ( x ) |
Regla de cambio de base de logaritmo |
log b ( c ) = 1 / log c ( b ) |
Regla de cambio de base de logaritmos |
log b ( x ) = log c ( x ) / log c ( b ) |
Derivada del logaritmo |
f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b )) |
Integral de logaritmo |
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C |
Logaritmo de número negativo |
log b ( x ) no está definido cuando x ≤ 0 |
Logaritmo de 0 |
log b (0) no está definido |
Logaritmo de 1 |
log b (1) = 0 |
Logaritmo de la base |
log b ( b ) = 1 |
Logaritmo del infinito |
lim log b ( x ) = ∞, cuando x → ∞ |
Ver: reglas de logaritmos
Regla de producto de logaritmo
El logaritmo de la multiplicación de xey es la suma del logaritmo de xy el logaritmo de y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Por ejemplo:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Regla del cociente de logaritmos
El logaritmo de la división de xey es la diferencia del logaritmo de xy el logaritmo de y.
log b ( x / y ) = log b ( x ) - log b ( y )
Por ejemplo:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Regla de potencia de logaritmo
El logaritmo de x elevado a la potencia de y es y multiplicado por el logaritmo de x.
log b ( x y ) = y ∙ log b ( x )
Por ejemplo:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Regla de cambio de base de logaritmo
El logaritmo en base b de c es 1 dividido por el logaritmo en base c de b.
log b ( c ) = 1 / log c ( b )
Por ejemplo:
log 2 (8) = 1 / log 8 (2)
Regla de cambio de base de logaritmos
El logaritmo en base b de x es el logaritmo en base c de x dividido por el logaritmo en base c de b.
log b ( x ) = log c ( x ) / log c ( b )
Por ejemplo, para calcular log 2 (8) en la calculadora, necesitamos cambiar la base a 10:
log 2 (8) = log 10 (8) / log 10 (2)
Ver: regla de cambio de base de registros
Logaritmo de número negativo
El logaritmo real en base b de x cuando x <= 0 no está definido cuando x es negativo o igual a cero:
log b ( x ) no está definido cuando x ≤ 0
Ver: registro de número negativo
Logaritmo de 0
El logaritmo en base b de cero no está definido:
log b (0) no está definido
El límite del logaritmo en base b de x, cuando x tiende a cero, es menos infinito:
![]()
Ver: logaritmo de cero
Logaritmo de 1
El logaritmo en base b de uno es cero:
log b (1) = 0
Por ejemplo, el logaritmo en base dos de uno es cero:
log 2 (1) = 0
Ver: registro de uno
Logaritmo del infinito
El límite del logaritmo en base b de x, cuando x se acerca al infinito, es igual al infinito:
lim log b ( x ) = ∞, cuando x → ∞
Logaritmo de la base
El logaritmo en base b de b es uno:
log b ( b ) = 1
Por ejemplo, el logaritmo en base dos de dos es uno:
log 2 (2) = 1
Derivada de logaritmo
Cuando
f ( x ) = log b ( x )
Entonces la derivada de f (x):
f ' ( x ) = 1 / ( x ln ( b ))
Ver: derivada logarítmica
Integral de logaritmo
La integral del logaritmo de x:
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
Por ejemplo:
∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) - 1 / ln (2) ) + C
Aproximación de logaritmos
log 2 ( x ) ≈ n + ( x / 2 n - 1),
Logaritmo complejo
Para el número complejo z:
z = re iθ = x + iy
El logaritmo complejo será (n = ...- 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
Problemas y respuestas de logaritmos
Problema # 1
Encuentra x para
log 2 ( x ) + log 2 ( x -3) = 2
Solución:
Usando la regla del producto:
log 2 ( x ∙ ( x -3)) = 2
Cambiar la forma del logaritmo según la definición del logaritmo:
x ∙ ( x -3) = 2 2
O
x 2 -3 x -4 = 0
Resolver la ecuación cuadrática:
x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1
Dado que el logaritmo no está definido para números negativos, la respuesta es:
x = 4
Problema # 2
Encuentra x para
log 3 ( x +2) - log 3 ( x ) = 2
Solución:
Usando la regla del cociente:
log 3 (( x +2) / x ) = 2
Cambiar la forma del logaritmo según la definición del logaritmo:
( x +2) / x = 3 2
O
x +2 = 9 x
O
8 x = 2
O
x = 0,25
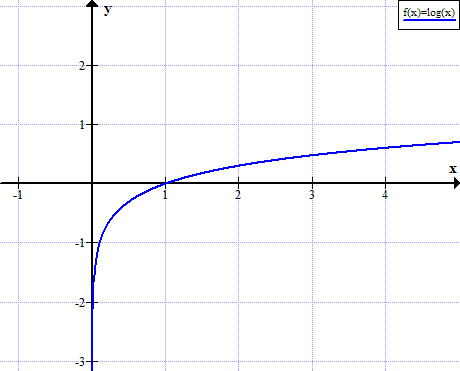
Gráfico de log (x)
log (x) no está definido para valores reales no positivos de x:
Tabla de logaritmos
| x | registro 10 x | registro 2 x | log e x |
|---|---|---|---|
| 0 | indefinido | indefinido | indefinido |
| 0 + | - ∞ | - ∞ | - ∞ |
| 0,0001 | -4 | -13.287712 | -9.210340 |
| 0,001 | -3 | -9.965784 | -6.907755 |
| 0,01 | -2 | -6.643856 | -4.605170 |
| 0,1 | -1 | -3.321928 | -2.302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0.301030 | 1 | 0,693147 |
| 3 | 0.477121 | 1.584963 | 1.098612 |
| 4 | 0,602060 | 2 | 1.386294 |
| 5 | 0,698970 | 2.321928 | 1.609438 |
| 6 | 0,778151 | 2.584963 | 1.791759 |
| 7 | 0.845098 | 2.807355 | 1.945910 |
| 8 | 0.903090 | 3 | 2.079442 |
| 9 | 0,954243 | 3.169925 | 2.197225 |
| 10 | 1 | 3.321928 | 2.302585 |
| 20 | 1.301030 | 4.321928 | 2.995732 |
| 30 | 1.477121 | 4.906891 | 3.401197 |
| 40 | 1,602060 | 5.321928 | 3.688879 |
| 50 | 1.698970 | 5.643856 | 3.912023 |
| 60 | 1.778151 | 5.906991 | 4.094345 |
| 70 | 1.845098 | 6.129283 | 4.248495 |
| 80 | 1.903090 | 6.321928 | 4.382027 |
| 90 | 1.954243 | 6.491853 | 4.499810 |
| 100 | 2 | 6.643856 | 4.605170 |
| 200 | 2.301030 | 7.643856 | 5.298317 |
| 300 | 2.477121 | 8.228819 | 5.703782 |
| 400 | 2.602060 | 8.643856 | 5.991465 |
| 500 | 2.698970 | 8.965784 | 6.214608 |
| 600 | 2.778151 | 9.228819 | 6.396930 |
| 700 | 2.845098 | 9.451211 | 6.551080 |
| 800 | 2.903090 | 9.643856 | 6.684612 |
| 900 | 2.954243 | 9.813781 | 6.802395 |
| 1000 | 3 | 9.965784 | 6.907755 |
| 10000 | 4 | 13.287712 | 9.210340 |
Ver también
- Reglas de logaritmos
- Cambio de logaritmo de base
- Logaritmo de cero
- Logaritmo de uno
- Logaritmo del infinito
- Logaritmo de número negativo
- Calculadora de logaritmos
- Gráfico de logaritmo
- Tabla de logaritmos
- Calculadora de logaritmos naturales
- Logaritmo natural - ln x
- e constante
- Decibel (dB)