Circunvolución

La convolución es la función de correlación de f (τ) con la función inversa g (t-τ).

El operador de convolución es el símbolo de asterisco * .

Convolución continua

La convolución de f (t) yg (t) es igual a la integral de f (τ) por f (t-τ):

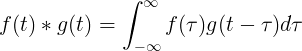
f (t) * g (t) = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) d \ tau

Convolución discreta

La convolución de 2 funciones discretas se define como:

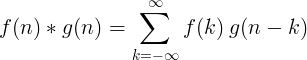
f (n) * g (n) = \ sum_ {k = - \ infty} ^ {\ infty} f (k) \: g (nk)

Convolución discreta 2D

La convolución discreta bidimensional se utiliza generalmente para el procesamiento de imágenes.

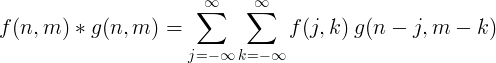
f (n, m) * g (n, m) = \ sum_ {j = - \ infty} ^ {\ infty} \ sum_ {k = - \ infty} ^ {\ infty} f (j, k) \: g (nj, mk)

Implementación de filtros con convolución

Podemos filtrar la señal de entrada discreta x (n) por convolución con la respuesta al impulso h (n) para obtener la señal de salida y (n).

y ( n ) = x ( n ) * h ( n )

Teorema de convolución

La transformada de Fourier de una multiplicación de 2 funciones es igual a la convolución de las transformadas de Fourier de cada función:

ℱ { f  ⋅ g } = ℱ { f } * ℱ { g }

La transformada de Fourier de una convolución de 2 funciones es igual a la multiplicación de las transformadas de Fourier de cada función:

ℱ { f  * g } = ℱ { f } ⋅ ℱ { g }

 
Teorema de convolución para transformada de Fourier continua

ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )

ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )

Teorema de convolución para la transformada discreta de Fourier

ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )

ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )

Teorema de convolución para la transformada de Laplace

ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )

 

Ver también

CÁLCULO
MESAS RÁPIDAS