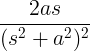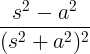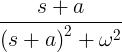Transformada de Laplace

La transformada de Laplace convierte una función en el dominio del tiempo en una función en el dominio s mediante la integración de cero a infinito

de la función en el dominio del tiempo, multiplicada por e ^-st .

La transformada de Laplace se utiliza para encontrar rápidamente soluciones para ecuaciones diferenciales e integrales.

La derivación en el dominio del tiempo se transforma en multiplicación por s en el dominio s.

La integración en el dominio del tiempo se transforma en división por s en el dominio s.

Función de transformación de Laplace

La transformada de Laplace se define con el operador L {}:

$F (s) = \ mathcal {L} \ left \ {f (t) \ right \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

La transformada inversa de Laplace se puede calcular directamente.

Por lo general, la transformación inversa se obtiene de la tabla de transformaciones.

Nombre de la función	Función de dominio del tiempo	Transformada de Laplace
Nombre de la función	f ( t )	F ( s ) = L { f ( t )}
Constante	1	$\ frac {1} {s}$
Lineal	t	$\ frac {1} {s ^ 2}$
Poder	t ⁿ	$\ frac {n!} {s ^ {n + 1}}$
Poder	t ^a	Γ ( a +1) ⋅ s ^{- ( a +1)}
Exponente	e ^en	$\ frac {1} {sa}$
Seno	pecar en	$\ frac {a} {s ^ 2 + a ^ 2}$
Coseno	porque en	$\ frac {s} {s ^ 2 + a ^ 2}$
Seno hiperbólico	sinh en	$\ frac {a} {s ^ 2-a ^ 2}$
Coseno hiperbólico	cosh en	$\ frac {s} {s ^ 2-a ^ 2}$
Seno creciente	t pecado en	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
Coseno creciente	t cos en	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
Seno en descomposición	e ^-at sin ωt	$\ frac {\ omega} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
Coseno en descomposición	e ^-at cos ωt	$\ frac {s + a} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
Función delta	δ ( t )	1
Delta retardado	δ ( ta )	e ^-as

Nombre de la propiedad	Función de dominio del tiempo	Transformada de Laplace	Comentario
	f ( t )	F ( s )
Linealidad	af ( t ) + bg ( t )	aF ( s ) + bG ( s )	a , b son constantes
Cambio de escala	f ( en )	$\ frac {1} {a} F \ left (\ frac {s} {a} \ right)$	a / 0
Cambio	e ^-at f ( t )	F ( s + a )
Retrasar	f ( ta )	e ^{- como} F ( s )
Derivación	$\ frac {df (t)} {dt}$	sF ( s ) - f (0)
Derivación N-ésima	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
Poder	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
Integración	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F (s)$
Recíproco	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
Circunvolución	f ( t ) * g ( t )	F ( s ) ⋅ G ( s )	* es el operador de convolución
Función periódica	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$