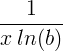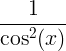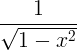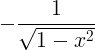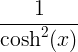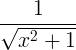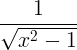Reglas derivadas

Reglas y leyes derivadas. Tabla de derivadas de funciones.

• Definición de derivada
• Reglas derivadas
• Tabla de derivadas de funciones
• Ejemplos de derivados

Definición de derivada

La derivada de una función es la razón de la diferencia del valor de la función f (x) en los puntos x + Δx yx con Δx, cuando Δx es infinitesimalmente pequeño. La derivada es la función pendiente o pendiente de la recta tangente en el punto x.

 

Segunda derivada

La segunda derivada viene dada por:

O simplemente deriva la primera derivada:

Derivada nth

El n º derivada se calcula mediante la derivación de f (x) n veces.

La n- ésima derivada es igual a la derivada de la derivada (n-1):

f ^{( n )} ( x ) = [ f ^{( n -1)} ( x )] '

Ejemplo:

Encuentra la cuarta derivada de

f ( x ) = 2 x ⁵

f ⁽⁴⁾ ( x ) = [2 x ⁵ ] '' '' = [10 x ⁴ ] '' '= [40 x ³ ]' '= [120 x ² ]' = 240 x

Derivada en gráfica de función

La derivada de una función es la pendiente de la línea tangencial.

Reglas derivadas

Regla de suma derivada	( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Regla del producto derivado	( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Regla del cociente derivado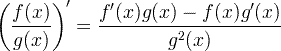
Regla de la cadena derivada	f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Regla de suma derivada

Cuando una y b son constantes.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Ejemplo:

Encuentra la derivada de:

3 x ² + 4 x.

Según la regla de la suma:

a = 3, b = 4

f ( x ) = x ² , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x ² + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Regla del producto derivado

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Regla del cociente derivado

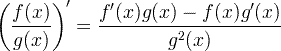
Regla de la cadena derivada

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Esta regla se puede entender mejor con la notación de Lagrange:

Aproximación lineal de funciones

Para Δx pequeño, podemos obtener una aproximación af (x ₀ + Δx), cuando conocemos f (x ₀ ) y f '(x ₀ ):

f ( x ₀ + Δ x ) ≈ f ( x ₀ ) + f '( x ₀ ) ⋅Δ x

Tabla de derivadas de funciones

Nombre de la función	Función	Derivado
	f ( x )	f '( x )
Constante	constante	0
Lineal	x	1
Poder	x a	hacha a- 1
Exponencial	e x	e x
Exponencial	una x	a x ln a
Logaritmo natural	en ( x )
Logaritmo	log b ( x )
Seno	pecado x	cos x
Coseno	cos x	-pecado x
Tangente	bronceado x
Arcsine	arcos en x
Arccosine	arccos x
Arctangent	arctan x
Seno hiperbólico	sinh x	cosh x
Coseno hiperbólico	cosh x	sinh x
Tangente hiperbólica	tanh x
Seno hiperbólico inverso	sinh -1 x
Coseno hiperbólico inverso	cosh -1 x
Tangente hiperbólica inversa	tanh -1 x

Ejemplos de derivados

Ejemplo 1

f ( x ) = x ³ +5 x ² + x +8

f ' ( x ) = 3 x ² + 2⋅5 x + 1 + 0 = 3 x ² +10 x +1

Ejemplo # 2

f ( x ) = sin (3 x ² )

Al aplicar la regla de la cadena:

f ' ( x ) = cos (3 x ² ) ⋅ [3 x ² ]' = cos (3 x ² ) ⋅ 6 x

Prueba de la segunda derivada

Cuando la primera derivada de una función es cero en el punto x ₀ .

f '( x ₀ ) = 0

Entonces la segunda derivada en el punto x ₀ , f '' (x ₀ ), puede indicar el tipo de ese punto:

 

f '' ( x 0 )/ 0	mínimo local
f '' ( x 0 ) <0	máximo local
f '' ( x 0 ) = 0	indeterminado

 

---

Ver también

• Cálculo
• Transformada de Laplace ( ℒ  )
• Símbolos de cálculo