e constante
La constante o el número de Euler es una constante matemática. La constante e es un número real e irracional.
e = 2,718281828459 ...
Definición de e
La constante e se define como el límite:
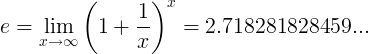
Definiciones alternativas
La constante e se define como el límite:
![]()
La constante e se define como la serie infinita:
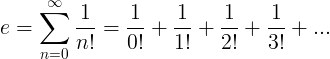
Propiedades de e
Recíproco de e
El recíproco de e es el límite:
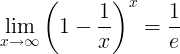
Derivadas de e
La derivada de la función exponencial es la función exponencial:
( e x ) '= e x
La derivada de la función logaritmo natural es la función recíproca:
(log e x ) '= (ln x )' = 1 / x
Integrales de e
La integral indefinida de la función exponencial e x es la función exponencial e x .
∫ e x dx = e x + c
La integral indefinida de la función logaritmo natural log e x es:
∫ log e x dx = ∫ ln x dx = x ln x - x + c
La integral definida de 1 ae de la función recíproca 1 / x es 1:
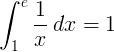
Logaritmo base e
El logaritmo natural de un número x se define como el logaritmo en base e de x:
ln x = log e x
Funcion exponencial
La función exponencial se define como:
f ( x ) = exp ( x ) = e x
Fórmula de Euler
El número complejo e iθ tiene la identidad:
e yoθ = cos ( θ ) + yo pecado ( θ )
i es la unidad imaginaria (la raíz cuadrada de -1).
θ es cualquier número real.
Ver también
- ¿Cómo e es 2,71828183?
- Reglas de logaritmos
- Logaritmo natural
- Reglas de exponentes
- Distribución normal
- Constante Pi
- e constante - wikipedia