ക്വാഡ്രാറ്റിക് സമവാക്യം
3 ഗുണകങ്ങളുള്ള രണ്ടാമത്തെ ഓർഡർ പോളിനോമിയലാണ് ക്വാഡ്രാറ്റിക് സമവാക്യം - a , b , c .
ക്വാഡ്രാറ്റിക് സമവാക്യം നൽകുന്നത്:
കോടാലി 2 + bx + c = 0
ക്വാഡ്രാറ്റിക് സമവാക്യത്തിനുള്ള പരിഹാരം x 1 , x 2 എന്നീ 2 അക്കങ്ങൾ നൽകുന്നു .
നമുക്ക് ക്വാഡ്രാറ്റിക് സമവാക്യം ഇനിപ്പറയുന്ന രൂപത്തിലേക്ക് മാറ്റാൻ കഴിയും:
( x - x 1 ) ( x - x 2 ) = 0
ക്വാഡ്രാറ്റിക് ഫോർമുല
ക്വാഡ്രാറ്റിക് സമവാക്യത്തിന് പരിഹാരം നൽകുന്നത് ക്വാഡ്രാറ്റിക് ഫോർമുലയാണ്:
![]()
സ്ക്വയർ റൂട്ടിനുള്ളിലെ പദപ്രയോഗത്തെ വിവേചനം എന്ന് വിളിക്കുന്നു , ഇതിനെ by:
= ബി 2 - 4 ഏ
വിവേചനരഹിതമായ നൊട്ടേഷനോടുകൂടിയ ക്വാഡ്രാറ്റിക് ഫോർമുല:
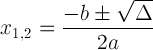
ഈ പദപ്രയോഗം പ്രധാനമാണ്, കാരണം ഇതിന് പരിഹാരത്തെക്കുറിച്ച് ഞങ്ങളോട് പറയാൻ കഴിയും:
- Δ/ 0 ആയിരിക്കുമ്പോൾ, 2 യഥാർത്ഥ വേരുകൾ x 1 = (- b + √ Δ ) / (2a) x 2 = (- b-√ Δ ) / (2a) ഉണ്ട് .
- Δ = 0 ആയിരിക്കുമ്പോൾ, ഒരു റൂട്ട് x 1 = x 2 = -b / (2a) ഉണ്ട് .
- : Δ <0, ഒരു യഥാർത്ഥ വേരുകൾ വരുമ്പോൾ, 2 മിശ്രസംഖ്യാമൂലങ്ങൾ ഉണ്ട്
X 1 (- ബി + ഇ√ = -Δ ) / (2a), x 2 = (- ബി√ -Δ ) / (2a) .
പ്രശ്നം # 1
3 x 2 +5 x +2 = 0
പരിഹാരം:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
പ്രശ്നം # 2
3 x 2 -6 x +3 = 0
പരിഹാരം:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
പ്രശ്നം # 3
x 2 +2 x +5 = 0
പരിഹാരം:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
യഥാർത്ഥ പരിഹാരങ്ങളൊന്നുമില്ല. മൂല്യങ്ങൾ സങ്കീർണ്ണ സംഖ്യകളാണ്:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
ക്വാഡ്രാറ്റിക് ഫംഗ്ഷൻ ഗ്രാഫ്
ക്വാഡ്രാറ്റിക് ഫംഗ്ഷൻ രണ്ടാമത്തെ ഓർഡർ പോളിനോമിയൽ ഫംഗ്ഷനാണ്:
f ( x ) = കോടാലി 2 + bx + c
ക്വാഡ്രാറ്റിക് സമവാക്യത്തിനുള്ള പരിഹാരങ്ങൾ ക്വാഡ്രാറ്റിക് ഫംഗ്ഷന്റെ വേരുകളാണ്, അവ എക്സ്-ആക്സിസുള്ള ക്വാഡ്രാറ്റിക് ഫംഗ്ഷൻ ഗ്രാഫിന്റെ ഇന്റർസെക്ഷൻ പോയിന്റുകളാണ്, എപ്പോൾ
f ( x ) = 0
എക്സ്-ആക്സിസിനൊപ്പം ഗ്രാഫിന്റെ 2 ഇന്റർസെക്ഷൻ പോയിന്റുകൾ ഉള്ളപ്പോൾ, ക്വാഡ്രാറ്റിക് സമവാക്യത്തിന് 2 പരിഹാരങ്ങളുണ്ട്.
എക്സ്-ആക്സിസിനൊപ്പം ഗ്രാഫിന്റെ 1 ഇന്റർസെക്ഷൻ പോയിന്റ് ഉള്ളപ്പോൾ, ക്വാഡ്രാറ്റിക് സമവാക്യത്തിന് 1 പരിഹാരമുണ്ട്.
എക്സ്-ആക്സിസിനൊപ്പം ഗ്രാഫിന്റെ ഇന്റർസെക്ഷൻ പോയിൻറുകൾ ഇല്ലാത്തപ്പോൾ, ഞങ്ങൾക്ക് യഥാർത്ഥ പരിഹാരങ്ങൾ (അല്ലെങ്കിൽ 2 സങ്കീർണ്ണ പരിഹാരങ്ങൾ) ലഭിക്കില്ല.