ലോഗരിതം നിയമങ്ങൾ

അടിസ്ഥാന ബി ലോഗരിതം ഒരു എണ്ണം ആണ് ഘാതാംഗമോ നാം ഉയർത്താൻ ചെയ്യേണ്ട അടിസ്ഥാന നമ്പർ നേടാൻ.

ലോഗരിതം നിർവചനം

B യെ y യുടെ ശക്തിയിലേക്ക് ഉയർത്തുമ്പോൾ x തുല്യമാണ്:

b y = x

X- ന്റെ അടിസ്ഥാന b ലോഗരിതം y ന് തുല്യമാണ്:

ലോഗ് ബി ( x ) = y

ഉദാഹരണത്തിന് എപ്പോൾ:

2 4 = 16

പിന്നെ

ലോഗ് 2 (16) = 4

എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷന്റെ വിപരീത പ്രവർത്തനമായി ലോഗരിതം

ലോഗരിഥമിക് പ്രവർത്തനം,

y = ലോഗ് ബി ( x )

എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്‌ഷന്റെ വിപരീത പ്രവർത്തനം,

x = b y

X (x/ 0) ന്റെ ലോഗരിതത്തിന്റെ എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്ഷൻ കണക്കാക്കിയാൽ,

f ( f -1 ( x )) = b ലോഗ് b ( x ) = x

അല്ലെങ്കിൽ x- ന്റെ എക്‌സ്‌പോണൻഷ്യൽ ഫംഗ്ഷന്റെ ലോഗരിതം കണക്കാക്കിയാൽ,

f -1 ( f ( x )) = ലോഗ് ബി ( ബി x ) = x

സ്വാഭാവിക ലോഗരിതം (ln)

സ്വാഭാവിക ലോഗരിതം അടിസ്ഥാനത്തിലേക്കുള്ള ഒരു ലോഗരിതം ആണ്:

ln ( x ) = ലോഗ് ഇ ( x )

എപ്പോഴാണ് ഇ നിരന്തരമായ നമ്പർ ഇതാണ്:

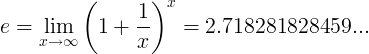
e = \ lim_ {x \ വലതുവശത്ത് \ infty} \ ഇടത് (1+ \ frac {1} {x} \ വലത്) ^ x = 2.718281828459 ...

അല്ലെങ്കിൽ

e = \ lim_ {x \ വലത് 0} \ ഇടത് (1+ \ വലത് x) ^ \ frac {1} {x}

 

കാണുക: സ്വാഭാവിക ലോഗരിതം

വിപരീത ലോഗരിതം കണക്കുകൂട്ടൽ

വിപരീത ലോഗരിതം (അല്ലെങ്കിൽ ആന്റി ലോഗരിതം) കണക്കാക്കുന്നത് അടിസ്ഥാന ബി ലോഗരിതത്തിലേക്ക് ഉയർത്തുന്നതിലൂടെയാണ്:

x = ലോഗ് -1 ( y ) = b y

ലോഗരിഥമിക് പ്രവർത്തനം

ലോഗരിഥമിക് ഫംഗ്ഷന് ഇതിന്റെ അടിസ്ഥാന രൂപം ഉണ്ട്:

f ( x ) = ലോഗ് ബി ( x )

ലോഗരിതം നിയമങ്ങൾ

റൂളിന്റെ പേര് ഭരണം
ലോഗരിതം ഉൽപ്പന്ന നിയമം
 ലോഗ് ബി ( x y ) = ലോഗ് ബി ( എക്സ് ) + ലോഗ് ബി ( വൈ )
ലോഗരിതം ഘടക നിയമം
 ലോഗ് ബി ( x / y ) = ലോഗ് ബി ( എക്സ് ) - ലോഗ് ബി ( വൈ )
ലോഗരിതം പവർ റൂൾ
 ലോഗ് ബി ( x y ) = y ലോഗ് ബി ( x )
ലോഗരിതം ബേസ് സ്വിച്ച് റൂൾ
 ലോഗ് ബി ( സി ) = 1 / ലോഗ് സി ( ബി )
ലോഗരിതം അടിസ്ഥാന മാറ്റ നിയമം
 ലോഗ് ബി ( എക്സ് ) = ലോഗ് സി ( എക്സ് ) / ലോഗ് സി ( ബി )
ലോഗരിതം ഡെറിവേറ്റീവ്
 f ( x ) = ലോഗ് ബി ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b ))
ലോഗരിതം സമന്വയിപ്പിക്കുന്നു
 ∫ ലോഗ് ബി ( x ) dx = x ∙ (ലോഗ് ബി ( x ) - 1 / ln ( ബി ) ) + സി
നെഗറ്റീവ് സംഖ്യയുടെ ലോഗരിതം
 x ≤ 0 ആയിരിക്കുമ്പോൾ ലോഗ് ബി ( x ) നിർവചിക്കപ്പെട്ടിട്ടില്ല
0 ന്റെ ലോഗരിതം
 ലോഗ് ബി (0) നിർ‌വ്വചിച്ചിട്ടില്ല
\ lim_ {x \ മുതൽ 0 ^ +} \ ടെക്സ്റ്റ്അപ്പ് {ലോഗ്} _b (x) = - \ infty
1 ന്റെ ലോഗരിതം
 ലോഗ് ബി (1) = 0
അടിസ്ഥാനത്തിന്റെ ലോഗരിതം
 ലോഗ് ബി ( ബി ) = 1
അനന്തതയുടെ ലോഗരിതം
 LIM ലോഗ് ബി ( X ) = ∞, എപ്പോൾ X → ∞

കാണുക: ലോഗരിതം നിയമങ്ങൾ

 

ലോഗരിതം ഉൽപ്പന്ന നിയമം

X, y എന്നിവയുടെ ഗുണനത്തിന്റെ ലോഗരിതം x ന്റെ ലോഗരിതം, y യുടെ ലോഗരിതം എന്നിവയുടെ ആകെത്തുകയാണ്.

ലോഗ് ബി ( x y ) = ലോഗ് ബി ( എക്സ് ) + ലോഗ് ബി ( വൈ )

ഉദാഹരണത്തിന്:

ലോഗ് 10 (3 ∙ 7) = ലോഗ് 10 (3) + ലോഗ് 10 (7)

ലോഗരിതം ഘടക നിയമം

X, y എന്നിവയുടെ വിഭജനത്തിന്റെ ലോഗരിതം x ന്റെ ലോഗരിതം, y ന്റെ ലോഗരിതം എന്നിവയുടെ വ്യത്യാസമാണ്.

ലോഗ് ബി ( x / y ) = ലോഗ് ബി ( എക്സ് ) - ലോഗ് ബി ( വൈ )

ഉദാഹരണത്തിന്:

ലോഗ് 10 (3 / 7) = ലോഗ് 10 (3) - രേഖ 10 (7)

ലോഗരിതം പവർ റൂൾ

Y- ന്റെ ശക്തിയിലേക്ക് ഉയർത്തിയ x- ന്റെ ലോഗരിതം x- ന്റെ ലോഗരിതത്തിന്റെ y ഇരട്ടിയാണ്.

ലോഗ് ബി ( x y ) = y ലോഗ് ബി ( x )

ഉദാഹരണത്തിന്:

ലോഗ് 10 (2 8 ) = 8 ∙ ലോഗ് 10 (2)

ലോഗരിതം ബേസ് സ്വിച്ച് റൂൾ

സി യുടെ അടിസ്ഥാന ബി ലോഗരിതം 1 ന്റെ അടിസ്ഥാന സി ലോഗരിതം കൊണ്ട് ഹരിക്കുന്നു.

ലോഗ് ബി ( സി ) = 1 / ലോഗ് സി ( ബി )

ഉദാഹരണത്തിന്:

ലോഗ് 2 (8) = 1 / ലോഗ് 8 (2)

ലോഗരിതം അടിസ്ഥാന മാറ്റ നിയമം

X- ന്റെ അടിസ്ഥാന ബി ലോഗരിതം x- ന്റെ അടിസ്ഥാന സി ലോഗരിതം ആണ്, അതിനെ b യുടെ അടിസ്ഥാന സി ലോഗരിതം കൊണ്ട് ഹരിക്കുന്നു.

ലോഗ് ബി ( എക്സ് ) = ലോഗ് സി ( എക്സ് ) / ലോഗ് സി ( ബി )

ഉദാഹരണത്തിന്, കാൽക്കുലേറ്ററിലെ ലോഗ് 2 (8) കണക്കാക്കാൻ, ഞങ്ങൾ അടിസ്ഥാനം 10 ആയി മാറ്റേണ്ടതുണ്ട്:

ലോഗ് 2 (8) = ലോഗ് 10 (8) / ലോഗ് 10 (2)

കാണുക: ലോഗ് അടിസ്ഥാന മാറ്റ നിയമം

നെഗറ്റീവ് സംഖ്യയുടെ ലോഗരിതം

X നെഗറ്റീവ് അല്ലെങ്കിൽ പൂജ്യത്തിന് തുല്യമാകുമ്പോൾ x <= 0 നിർവചിക്കപ്പെടാത്തപ്പോൾ x ന്റെ അടിസ്ഥാന ബി യഥാർത്ഥ ലോഗരിതം:

x ≤ 0 ആയിരിക്കുമ്പോൾ ലോഗ് ബി ( x ) നിർവചിക്കപ്പെട്ടിട്ടില്ല

കാണുക: നെഗറ്റീവ് നമ്പറിന്റെ ലോഗ്

0 ന്റെ ലോഗരിതം

പൂജ്യത്തിന്റെ അടിസ്ഥാന ബി ലോഗരിതം നിർവചിക്കപ്പെട്ടിട്ടില്ല:

ലോഗ് ബി (0) നിർ‌വ്വചിച്ചിട്ടില്ല

X പൂജ്യത്തോട് അടുക്കുമ്പോൾ x ന്റെ അടിസ്ഥാന ബി ലോഗരിതത്തിന്റെ പരിധി മൈനസ് അനന്തമാണ്:

\ lim_ {x \ മുതൽ 0 ^ +} \ ടെക്സ്റ്റ്അപ്പ് {ലോഗ്} _b (x) = - \ infty

കാണുക: പൂജ്യത്തിന്റെ ലോഗ്

1 ന്റെ ലോഗരിതം

ഒന്നിന്റെ അടിസ്ഥാന ബി ലോഗരിതം പൂജ്യമാണ്:

ലോഗ് ബി (1) = 0

ഉദാഹരണത്തിന്, ഒന്നിന്റെ രണ്ട് അടിസ്ഥാന ലോഗരിതം പൂജ്യമാണ്:

ലോഗ് 2 (1) = 0

കാണുക: ഒന്നിന്റെ ലോഗ്

അനന്തതയുടെ ലോഗരിതം

X അനന്തതയിലേക്ക് അടുക്കുമ്പോൾ x ന്റെ അടിസ്ഥാന ബി ലോഗരിതത്തിന്റെ പരിധി അനന്തതയ്ക്ക് തുല്യമാണ്:

LIM ലോഗ് ബി ( X ) = ∞, എപ്പോൾ X → ∞

കാണുക: അനന്തതയുടെ ലോഗ്

അടിസ്ഥാനത്തിന്റെ ലോഗരിതം

B യുടെ അടിസ്ഥാന ബി ലോഗരിതം ഒന്നാണ്:

ലോഗ് ബി ( ബി ) = 1

ഉദാഹരണത്തിന്, രണ്ടിന്റെ അടിസ്ഥാന രണ്ട് ലോഗരിതം ഒന്നാണ്:

ലോഗ് 2 (2) = 1

ലോഗരിതം ഡെറിവേറ്റീവ്

എപ്പോൾ

f ( x ) = ലോഗ് ബി ( x )

അപ്പോൾ f (x) ന്റെ ഡെറിവേറ്റീവ്:

f ' ( x ) = 1 / ( x ln ( b ))

കാണുക: ലോഗ് ഡെറിവേറ്റീവ്

ലോഗരിതം ഇന്റഗ്രൽ

X- ന്റെ ലോഗരിതത്തിന്റെ സമഗ്രത:

∫ ലോഗ് ബി ( x ) dx = x ∙ (ലോഗ് ബി ( x ) - 1 / ln ( ബി ) ) + സി

ഉദാഹരണത്തിന്:

∫ ലോഗ് 2 ( x ) dx = x ∙ (ലോഗ് 2 ( x ) - 1 / ln (2) ) + സി

ലോഗരിതം ഏകദേശീകരണം

ലോഗ് 2 ( x ) ≈ n + ( x / 2 n - 1),

സങ്കീർണ്ണ ലോഗരിതം

സങ്കീർണ്ണ സംഖ്യയ്ക്ക് z:

z = re iθ = x + iy

സങ്കീർണ്ണമായ ലോഗരിതം ഇതായിരിക്കും (n = ...- 2, -1,0,1,2, ...):

ലോഗ് z = ln ( r ) + i ( θ + 2nπ ) = ln ( x ( x 2 + y 2 )) + i · arctan ( y / x ))

ലോഗരിതം പ്രശ്‌നങ്ങളും ഉത്തരങ്ങളും

പ്രശ്നം # 1

ഇതിനായി x കണ്ടെത്തുക

ലോഗ് 2 ( x ) + ലോഗ് 2 ( x -3) = 2

പരിഹാരം:

ഉൽപ്പന്ന നിയമം ഉപയോഗിക്കുന്നു:

ലോഗ് 2 ( x ( x -3)) = 2

ലോഗരിതം നിർവചനം അനുസരിച്ച് ലോഗരിതം ഫോം മാറ്റുന്നു:

x ( x -3) = 2 2

അല്ലെങ്കിൽ

x 2 -3 x -4 = 0

ക്വാഡ്രാറ്റിക് സമവാക്യം പരിഹരിക്കുന്നു:

x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1

നെഗറ്റീവ് നമ്പറുകൾക്കായി ലോഗരിതം നിർവചിച്ചിട്ടില്ലാത്തതിനാൽ, ഉത്തരം:

x = 4

പ്രശ്നം # 2

ഇതിനായി x കണ്ടെത്തുക

ലോഗ് 3 ( x +2) - ലോഗ് 3 ( x ) = 2

പരിഹാരം:

ഘടക നിയമം ഉപയോഗിക്കുന്നു:

ലോഗ് 3 (( x +2) / x ) = 2

ലോഗരിതം നിർവചനം അനുസരിച്ച് ലോഗരിതം ഫോം മാറ്റുന്നു:

( x +2) / x = 3 2

അല്ലെങ്കിൽ

x +2 = 9 x

അല്ലെങ്കിൽ

8 x = 2

അല്ലെങ്കിൽ

x = 0.25

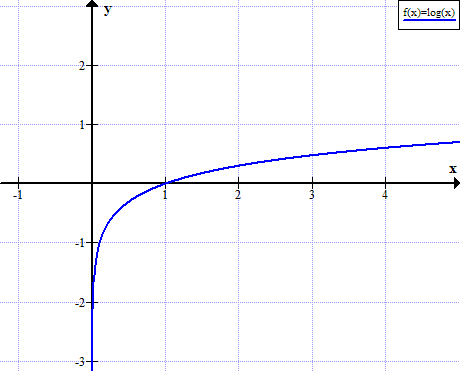
ലോഗിന്റെ ഗ്രാഫ് (x)

x ന്റെ യഥാർത്ഥ പോസിറ്റീവ് അല്ലാത്ത മൂല്യങ്ങൾക്കായി ലോഗ് (x) നിർവചിച്ചിട്ടില്ല:

ലോഗരിതംസ് പട്ടിക

x ലോഗ് 10 x ലോഗ് 2 x ലോഗ് ഇ x
0 നിർവചിച്ചിട്ടില്ല നിർവചിച്ചിട്ടില്ല നിർവചിച്ചിട്ടില്ല
0 + - - -
0.0001 -4 -13.287712 -9.210340
0.001 -3 -9.965784 -6.907755
0.01 -2 -6.643856 -4.605170
0.1 -1 -3.321928 -2.302585
1 0 0 0
2 0.301030 1 0.693147
3 0.477121 1.584963 1.098612
4 0.602060 2 1.386294
5 0.698970 2.321928 1.609438
6 0.778151 2.584963 1.791759
7 0.845098 2.807355 1.945910
8 0.903090 3 2.079442
9 0.954243 3.169925 2.197225
10 1 3.321928 2.302585
20 1.301030 4.321928 2.995732
30 1.477121 4.906891 3.401197
40 1.602060 5.321928 3.688879
50 1.698970 5.643856 3.912023
60 1.778151 5.906991 4.094345
70 1.845098 6.129283 4.248495
80 1.903090 6.321928 4.382027
90 1.954243 6.491853 4.499810
100 2 6.643856 4.605170
200 2.301030 7.643856 5.298317
300 2.477121 8.228819 5.703782
400 2.602060 8.643856 5.991465
500 2.698970 8.965784 6.214608
600 2.778151 9.228819 6.396930
700 2.845098 9.451211 6.551080
800 2.903090 9.643856 6.684612
900 2.954243 9.813781 6.802395
1000 3 9.965784 6.907755
10000 4 13.287712 9.210340

 

ലോഗരിതം കാൽക്കുലേറ്റർ

 

ഇതും കാണുക

ആൽ‌ജിബ്ര
ദ്രുത പട്ടികകൾ