അടിസ്ഥാന പ്രോബബിലിറ്റി ഫോർമുലകൾ
പ്രോബബിലിറ്റി ശ്രേണി
0 ≤ P ( A ) ≤ 1
കോംപ്ലിമെന്ററി ഇവന്റുകളുടെ നിയമം
പി ( എ സി ) + പി ( എ ) = 1
കൂട്ടിച്ചേർക്കൽ നിയമം
P (A∪B) = P (A) + P (B) - P (A∩B)
ഇവന്റുകൾ നിരസിക്കുക
എ, ബി ഇവന്റുകൾ ഡിജോയിറ്റ് iff ആണ്
P (A∩B) = 0
സോപാധിക പ്രോബബിലിറ്റി
P (A | B) = P (A∩B) / P (B)
ബയേസ് ഫോർമുല
പി (എ | ബി) = പി (ബി | എ) ⋅ പി (എ) / പി (ബി)
സ്വതന്ത്ര ഇവന്റുകൾ
എ, ബി ഇവന്റുകൾ സ്വതന്ത്ര iff ആണ്
P (A∩B) = P (A) ⋅ P (B)
സഞ്ചിത വിതരണ പ്രവർത്തനം
എഫ് എക്സ് ( X ) = പി ( എക്സ് ≤ X )
പ്രോബബിലിറ്റി മാസ് ഫംഗ്ഷൻ
![]()
പ്രോബബിലിറ്റി ഡെൻസിറ്റി ഫംഗ്ഷൻ
![]()
![]()
![]()
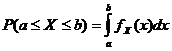
![]()
കോവിയറൻസ്
![]()
പരസ്പരബന്ധം
![]()
ബെർണൂലി: 0-പരാജയം 1-വിജയം
ജ്യാമിതീയ: 0-പരാജയം 1-വിജയം
ഹൈപ്പർജിയോമെട്രിക്: കെ വിജയ വസ്തുക്കളുള്ള N വസ്തുക്കൾ, n വസ്തുക്കൾ എടുക്കുന്നു.
പ്രോബബിലിറ്റി & സ്റ്റാറ്റിസ്റ്റിക്സ്
- അടിസ്ഥാന പ്രോബബിലിറ്റി
- പ്രതീക്ഷ
- വേരിയൻസ്
- അടിസ്ഥാന വ്യതിയാനം
- പ്രോബബിലിറ്റി വിതരണം
- സാധാരണ വിതരണം
- സ്ഥിതിവിവരക്കണക്ക് ചിഹ്നങ്ങൾ