പ്രോബബിലിറ്റി വിതരണം
പ്രോബബിലിറ്റിയിലും സ്റ്റാറ്റിസ്റ്റിക്സ് വിതരണത്തിലും ഒരു റാൻഡം വേരിയബിളിന്റെ സ്വഭാവമാണ്, ഓരോ മൂല്യത്തിലും റാൻഡം വേരിയബിളിന്റെ സംഭാവ്യത വിവരിക്കുന്നു.
ഓരോ വിതരണത്തിനും ഒരു നിശ്ചിത പ്രോബബിലിറ്റി ഡെൻസിറ്റി ഫംഗ്ഷനും പ്രോബബിലിറ്റി ഡിസ്ട്രിബ്യൂഷൻ ഫംഗ്ഷനുമുണ്ട്.
പ്രോബബിലിറ്റി വിതരണങ്ങളുടെ അനിശ്ചിതകാല എണ്ണം ഉണ്ടെങ്കിലും, പൊതുവായ നിരവധി വിതരണങ്ങൾ ഉപയോഗത്തിലുണ്ട്.
സഞ്ചിത വിതരണ പ്രവർത്തനം
എഫ് (എക്സ്) സഞ്ചിത വിതരണ ഫംഗ്ഷൻ പ്രോബബിലിറ്റി വിതരണത്തെ വിവരിക്കുന്നു,
ഇത് x- നേക്കാൾ ചെറുതോ തുല്യമോ ആയ മൂല്യം ലഭിക്കാൻ റാൻഡം വേരിയബിൾ X- ന്റെ സാധ്യതയാണ്:
എഫ് ( X ) = പി ( എക്സ് ≤ X )
തുടർച്ചയായ വിതരണം
തുടർച്ചയായ റാൻഡം വേരിയബിൾ എക്സിന്റെ പ്രോബബിലിറ്റി ഡെൻസിറ്റി ഫംഗ്ഷൻ എഫ് (യു) സംയോജിപ്പിച്ചാണ് എഫ് (എക്സ്) സഞ്ചിത വിതരണ പ്രവർത്തനം കണക്കാക്കുന്നത്.
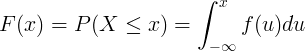
പ്രത്യേക വിതരണം
ഡിസ്ക്രീറ്റ് റാൻഡം വേരിയബിൾ എക്സിന്റെ പ്രോബബിലിറ്റി മാസ് ഫംഗ്ഷൻ പി (യു) ന്റെ സംഗ്രഹത്തിലൂടെയാണ് ക്യുമുലേറ്റീവ് ഡിസ്ട്രിബ്യൂഷൻ ഫംഗ്ഷൻ കണക്കാക്കുന്നത്.
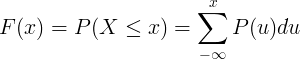
തുടർച്ചയായ വിതരണ പട്ടിക
തുടർച്ചയായ റാൻഡം വേരിയബിളിന്റെ വിതരണമാണ് തുടർച്ചയായ വിതരണം.
തുടർച്ചയായ വിതരണ ഉദാഹരണം
...
തുടർച്ചയായ വിതരണ പട്ടിക
| വിതരണത്തിന്റെ പേര് | വിതരണ ചിഹ്നം | പ്രോബബിലിറ്റി ഡെൻസിറ്റി ഫംഗ്ഷൻ (പിഡിഎഫ്) | ശരാശരി | വേരിയൻസ് |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = , Var ( എക്സ് ) |
||
| സാധാരണ / ഗാസിയൻ | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| ഒരേപോലെ | X ~ U ( a , b ) |
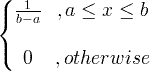 |
|
|
| എക്സ്പോണൻഷ്യൽ | X ~ exp () | |
|
|
| ഒബാമ | എക്സ് ~ ഗാമ ( സി ,) | 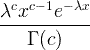 x / 0, സി / 0, λ/ 0 |
|
|
| ചി സ്ക്വയർ | X ~ χ 2 ( k ) |
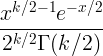 |
k |
2 കെ |
| വിഷാർട്ട് | ||||
| എഫ് | X ~ F ( k 1 , k 2 ) |
|||
| ബീറ്റ | ||||
| വെയ്ബുൾ | ||||
| ലോഗ്-നോർമൽ | X ~ LN (μ, σ 2 ) |
|||
| റെയ്ലെയ് | ||||
| കോച്ചി | ||||
| ഡിറിക്ലെറ്റ് | ||||
| ലാപ്ലേസ് | ||||
| ലെവി | ||||
| അരി | ||||
| വിദ്യാർത്ഥിയുടെ ടി |
വ്യതിരിക്ത വിതരണ പട്ടിക
റാൻഡം വേരിയബിളിന്റെ വിതരണമാണ് ഡിസ്ക്രീറ്റ് ഡിസ്ട്രിബ്യൂഷൻ.
വ്യതിരിക്ത വിതരണ ഉദാഹരണം
...
വ്യതിരിക്ത വിതരണ പട്ടിക
| വിതരണത്തിന്റെ പേര് | വിതരണ ചിഹ്നം | പ്രോബബിലിറ്റി മാസ് ഫംഗ്ഷൻ (pmf) | ശരാശരി | വേരിയൻസ് | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0,1,2, ... |
ഇ ( x ) | Var ( x ) | |||
| ദ്വിപദം | എക്സ് ~ ബിൻ ( n , പി ) |
|
np |
np (1- പി ) |
|
| വിഷം | എക്സ് ~ പോയസൺ (λ) |
|
λ 0 |
λ |
λ |
| ഒരേപോലെ | X ~ U ( a, b ) |
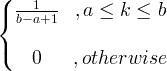 |
|
|
|
| ജ്യാമിതീയ | എക്സ് ~ ജിയോം ( പി ) |
|
|
|
|
| ഹൈപ്പർ-ജ്യാമിതീയ | X ~ HG ( N , K , n ) |
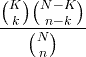 |
N = 0,1,2, ... കെ = 0,1, .., എൻ n = 0,1, ..., എൻ |
|
|
| ബെർണൂലി | എക്സ് ~ ബെർൺ ( പി ) |
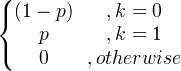 |
p |
p (1- പി ) |
|
ഇതും കാണുക
പ്രോബബിലിറ്റി & സ്റ്റാറ്റിസ്റ്റിക്സ്
- അടിസ്ഥാന പ്രോബബിലിറ്റി
- പ്രതീക്ഷ
- വേരിയൻസ്
- അടിസ്ഥാന വ്യതിയാനം
- പ്രോബബിലിറ്റി വിതരണം
- സാധാരണ വിതരണം
- സ്ഥിതിവിവരക്കണക്ക് ചിഹ്നങ്ങൾ
ദ്രുത പട്ടികകൾ