സ്റ്റാൻഡേർഡ് ഡീവിയേഷൻ

പ്രോബബിലിറ്റിയിലും സ്ഥിതിവിവരക്കണക്കിലും, റാൻഡം വേരിയബിളിന്റെ സ്റ്റാൻഡേർഡ് ഡീവിയേഷൻ എന്നത് ശരാശരി മൂല്യത്തിൽ നിന്ന് ഒരു റാൻഡം വേരിയബിളിന്റെ ശരാശരി ദൂരമാണ്.

റാൻഡം വേരിയബിൾ എങ്ങനെയാണ് ശരാശരി മൂല്യത്തിനടുത്ത് വിതരണം ചെയ്യുന്നതെന്ന് ഇത് പ്രതിനിധീകരിക്കുന്നു. റാൻഡം വേരിയബിൾ ശരാശരി മൂല്യത്തിനടുത്താണ് വിതരണം ചെയ്യുന്നതെന്ന് ചെറിയ സ്റ്റാൻഡേർഡ് ഡീവിയേഷൻ സൂചിപ്പിക്കുന്നു. റാൻഡം വേരിയബിൾ ശരാശരി മൂല്യത്തിൽ നിന്ന് വളരെ ദൂരെയാണ് വിതരണം ചെയ്യുന്നതെന്ന് വലിയ സ്റ്റാൻഡേർഡ് ഡീവിയേഷൻ സൂചിപ്പിക്കുന്നു.

സ്റ്റാൻഡേർഡ് ഡീവിയേഷൻ ഡെഫനിഷൻ ഫോർമുല

റാൻഡം വേരിയബിൾ എക്‌സിന്റെ വേരിയൻസിന്റെ സ്‌ക്വയർ റൂട്ടാണ് സ്റ്റാൻഡേർഡ് ഡീവിയേഷൻ, mean ന്റെ ശരാശരി മൂല്യം.

$\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}$

സ്റ്റാൻഡേർഡ് ഡീവിയേഷന്റെ നിർവചനത്തിൽ നിന്ന് നമുക്ക് ലഭിക്കും

$\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}$

തുടർച്ചയായ റാൻഡം വേരിയബിളിന്റെ സ്റ്റാൻഡേർഡ് ഡീവിയേഷൻ

ശരാശരി മൂല്യം μ, പ്രോബബിലിറ്റി ഡെൻസിറ്റി ഫംഗ്ഷൻ f (x) ഉള്ള തുടർച്ചയായ റാൻഡം വേരിയബിളിനായി:

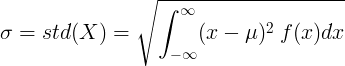
$\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}$

അല്ലെങ്കിൽ

$\ sigma = std (X) = \ sqrt {\ ഇടത് [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}.$

ഡിസ്ക്രീറ്റ് റാൻഡം വേരിയബിളിന്റെ സ്റ്റാൻഡേർഡ് ഡീവിയേഷൻ

ശരാശരി മൂല്യം μ, പ്രോബബിലിറ്റി മാസ് ഫംഗ്ഷൻ പി (x) ഉള്ള ഡിസ്‌ക്രീറ്റ് റാൻഡം വേരിയബിൾ എക്‌സിനായി:

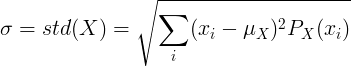
$\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}$

അല്ലെങ്കിൽ

$\ sigma = std (X) = \ sqrt {\ ഇടത് [\ sum_ {i} ^} x_i ^ 2P (x_i) \ വലത്] - \ mu ^ 2}$

പ്രോബബിലിറ്റി വിതരണം

സ്റ്റാൻഡേർഡ് ഡീവിയേഷൻ