चतुर्भुज समीकरण
चतुर्भुज समीकरण हे दुसरे ऑर्डर बहुपद आहे ज्यात 3 गुणांक आहेत - ए , बी , सी .
चतुर्भुज समीकरण दिले आहेः
ax 2 + bx + c = 0
चतुर्भुज समीकरणाचे समाधान 2 अंक x 1 आणि x 2 द्वारे दिले आहे .
आपण चौरस समीकरण या रुपात बदलू:
( x - x 1 ) ( x - x 2 ) = 0
चतुर्भुज फॉर्म्युला
चतुर्भुज समीकरणाचे समाधान द्विघात सूत्रानुसार दिले गेले आहे:
![]()
चौरस मुळाच्या अंतर्गत अभिव्यक्तीला भेदभाव म्हणतात आणि Δ द्वारे दर्शविले जाते:
Δ = बी 2 - 4 एसी
भेदभावी संकेतकेसह चौरस सूत्र:
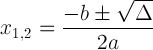
ही अभिव्यक्ती महत्त्वपूर्ण आहे कारण ती आम्हाला समाधानाबद्दल सांगू शकते:
- जेव्हा Δ/ 0, येथे 2 वास्तविक मुळे x 1 = (- बी + √ Δ ) / (2 ए) आणि एक्स 2 = (- बी-√ Δ ) / (2 ए) आहेत .
- जेव्हा Δ = 0, एक रूट x 1 = x 2 = -b / (2 अ) आहे .
- : Δ <0, खराखुरा मुळे आहेत, 2 जटिल मुळे आहेत
नाम 1 - (ब + i√ = -Δ आणि X / (2 अ)) 2 = (- bi√ -Δ ) / (2 अ) .
समस्या # 1
3 x 2 +5 x +2 = 0
उपाय:
a = 3, बी = 5, सी = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
समस्या # 2
3 x 2 -6 x +3 = 0
उपाय:
a = 3, बी = -6, सी = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
समस्या # 3
x 2 + 2 x +5 = 0
उपाय:
a = 1, बी = 2, सी = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
कोणतीही वास्तविक निराकरणे नाहीत. मूल्ये जटिल संख्या आहेत:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
चतुर्भुज फंक्शन आलेख
चतुर्भुज फंक्शन हे दुसर्या ऑर्डरचे बहुपद कार्य आहे:
f ( x ) = ax 2 + bx + c
चतुर्भुज समीकरणाचे निराकरण म्हणजे चतुष्कोला फंक्शनची मुळे, जी एक्स-अक्षासह चौरस फंक्शन ग्राफचे छेदनबिंदू असतात
f ( x ) = 0
जेव्हा एक्स-अक्षासह आलेखाचे दोन छेदनबिंदू असतात तेव्हा चतुष्पाद समीकरणाचे 2 निराकरण होते.
जेव्हा एक्स-अक्षासह आलेखाचा 1 छेदनबिंदू असतो तेव्हा चतुष्पाद समीकरणास 1 समाधान मिळतो.
जेव्हा एक्स-अक्षासह आलेखाचे कोणतेही छेदनबिंदू नसतात, तेव्हा आपल्याला वास्तविक निराकरणे (किंवा 2 जटिल सोल्यूशन) मिळत नाहीत.