नैसर्गिक लोगारिदम - एलएन (एक्स)

नॅचरल लॉगरिथम हे संख्येच्या बेस ई वर लॉगॅरिथम असते.

नैसर्गिक लॉगरिदम व्याख्या

कधी

e y = x

नंतर x चा बेस ई लोगारिदम आहे

ln ( x ) = लॉग e ( x ) = y

 

ई सतत किंवा यूलरची संख्या आहे:

ई ≈ 2.71828183

घातांकीय कार्याचे व्यस्त कार्य म्हणून एल.एन.

नॅचरल लॉगरिथम फंक्शन एलएन (एक्स) एक्सपोन्शियल फंक्शन ई एक्स चे व्यस्त कार्य आहे .

X/ 0 साठी

f ( f -1 ( x )) = e ln ( x ) = x

किंवा

f -1 ( f ( x )) = ln ( e x ) = x

नैसर्गिक लोगारिदम नियम आणि गुणधर्म

नियम नाव नियम उदाहरण
उत्पादन नियम

ln ( x ∙ y ) = ln ( x ) + ln ( y )

ln (3 ∙ 7) = ln (3) + ln (7)
उगम नियम

ln ( x / y ) = ln ( x ) - ln ( y )

यामध्ये (3 / 7) = इन (3) - यामध्ये (7)
शक्ती नियम

ln ( x y ) = y ∙ ln ( x )

ln (2 8 ) = 8 ∙ ln (2)
एलएन व्युत्पन्न
 f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x  
LN अविभाज्य
 ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C  
negativeणात्मक संख्या
 x ≤ 0 असताना ln ( x ) अपरिभाषित असते  
शून्य LN
 ln (0) अपरिभाषित आहे  
 
एक च्या LN
 ln (1) = 0  
अनंत LN
 लिम एलएन ( एक्स ) = ∞, जेव्हा एक्स → ∞  
युलरची ओळख ln (-1) = i π  

 

लोगारिदम उत्पादन नियम

X आणि y च्या गुणाकाराचा लॉगरिथम म्हणजे x च्या लॉगॅरिथम आणि y च्या लॉगेरिदमचे बेरीज.

लॉग बी ( x ∙ y ) = लॉग बी ( एक्स ) + लॉग बी ( वाय )

उदाहरणार्थ:

लॉग 10 (3 ∙ 7) = लॉग 10 (3) + लॉग 10 (7)

लोगारिदम क्वांटिएंट नियम

X आणि y च्या भागाचे लोगारिदम हे x च्या लॉगॅरिथम आणि y च्या लोगारिदममधील फरक आहे.

लॉग बी ( x / y ) = लॉग बी ( एक्स ) - लॉग बी ( वाय )

उदाहरणार्थ:

लॉग इन 10 (3 / 7) = लॉग इन 10 (3) - लॉग इन 10 (7)

लोगारिदम शक्ती नियम

Y च्या सामर्थ्यापर्यंत वाढविलेला x चा लॉगॅरिथम x च्या लॉगॅरिथमच्या y पट आहे.

लॉग बी ( x y ) = y ∙ लॉग बी ( एक्स )

उदाहरणार्थ:

लॉग 10 (2 8 ) = 8 ∙ लॉग 10 (2)

नैसर्गिक लॉगरिदमचे व्युत्पन्न

नेचरल लॉगरिथम फंक्शनचे व्युत्पन्न म्हणजे परस्पर क्रिया.

कधी

f ( x ) = ln ( x )

F (x) चे व्युत्पन्न आहे:

f ' ( x ) = 1 / x

नैसर्गिक लॉगरिदमचे अविभाज्य

नेचरल लॉगरिथम फंक्शनचे अविभाज्य खालीलप्रमाणे आहेः

कधी

f ( x ) = ln ( x )

F (x) चे अविभाज्य आहे:

∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C

0 चे Ln

शून्यचा नैसर्गिक लघुगणक अपरिभाषित आहे:

ln (0) अपरिभाषित आहे

X शून्य जवळ आल्यावर x च्या नैसर्गिक लॉगॅरिथमच्या 0 जवळची मर्यादा वजा अनंत आहेः

1 चे एल.एन.

एखाद्याचा नैसर्गिक लघुगणक शून्य आहे:

ln (1) = 0

अनंत Ln

अनंत जवळ आल्यावर अनंतपणाच्या नैसर्गिक लघुगणकांची मर्यादा अनंताइतकी असते:

लिम एलएन ( एक्स ) = ∞, जेव्हा एक्स → ∞

कॉम्प्लेक्स लॉगरिदम

जटिल संख्या z साठी:

z = रे iθ = x + iy

गुंतागुंतीचा लघुगणक (एन = ...- 2, -1,0,1,2, ...) असेल:

लॉग z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · आर्क्टन ( y / x ))

एलएन (एक्स) चा आलेख

x च्या वास्तविक अ-सकारात्मक मूल्यांसाठी ln (x) परिभाषित केलेले नाही:

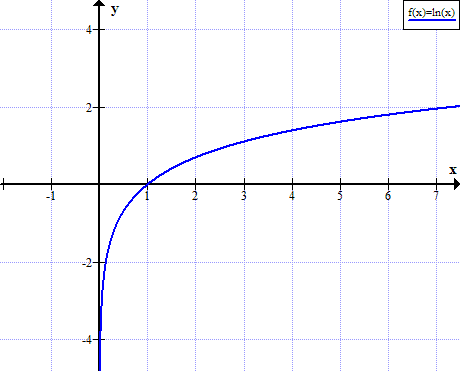
नैसर्गिक लॉगरिदम सारणी

x एलएन एक्स
0 अपरिभाषित
0 + - ∞
0.0001 -9.210340
0.001 -6.907755
0.01 -4.605170
0.1 -2.302585
1 0
2 0.693147
ई ≈ 2.7183 1
3 | 1.098612
4 1.386294
5 1.609438
6 1.791759
7 1.945910
8 2.079442
9 2.197225
10 2.302585
20 2.995732
30 3.401197
40 3.688879
50 3.912023
60 4.094345
70 4.248495
80 4.382027
90 4.499810
100 4.605170
200 5.298317
300 5.703782
400 5.991465
500 6.214608
600 6.396930
700 6.551080
800 6.684612
900 6.802395
1000 6.907755
10000 9.210340

 

लॉगरिदमचे नियम ►

 

हे देखील पहा

अल्जीब्रा
वेगवान सारण्या