कन्व्होल्यूशन

कन्व्होल्यूशन हे उलट (फ-τ) चे परस्पर क्रिया फंक्शन जी (टी-τ) सह परस्परसंबंध कार्य करते.

कन्व्होल्यूशन ऑपरेटर तारांकित प्रतीक * आहे .

F (t) आणि g (t) चे एकत्रीकरण f (τ) वेळा f (t-τ) च्या अविभाज्यतेसारखे आहे:

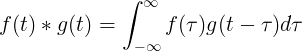
$f (t) * g (t) = \ int _ {- ty infty} ^ {\ infty} f (au tau) g (t- \ tau) d \ tau$

2 वेगळ्या फंक्शन्सची रूपांतरण खालीलप्रमाणे आहे:

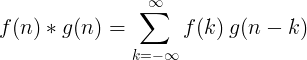
$f (n) * g (n) = \ sum_ {k = - \ infty} ^ {\ infty} f (k) \: g (nk)$

2 मितीय डिस्क्रेट कॉन्व्होल्यूशन सामान्यतः प्रतिमा प्रक्रियेसाठी वापरला जातो.

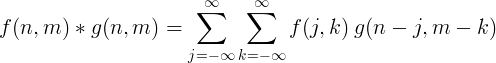
$f (n, m) * g (n, m) = \ sum_ {j = - \ infty} ^ {\ infty} \ sum_ {k = - \ infty} ^ {\ infty} f (j, k) \: ग्रॅम (एनजे, एमके)$

आउटपुट सिग्नल y (n) मिळविण्यासाठी आम्ही आडवा प्रतिसाद एच (एन) सह विल्हेवाट लावून (स्वतंत्र) इनपुट सिग्नल x (n) फिल्टर करू शकतो.

y ( n ) = x ( n ) * एच ( एन )

2 फंक्शन्सच्या गुणाकाराचे फूरियर ट्रान्सफॉर्म प्रत्येक फंक्शनच्या फुरियर ट्रान्सफॉर्मच्या कन्व्होल्यूशनच्या समतुल्य आहे:

ℱ { एफ ⋅ जी } = ℱ { एफ } * ℱ { जी }

2 फंक्शन्सच्या रूपांतरणाचे फुरियर ट्रान्सफॉर्म प्रत्येक फंक्शनच्या फूरियर ट्रान्सफॉर्मच्या गुणाकारापेक्षा समान असते:

ℱ { फ * ग्रॅम } = ℱ { फ } ⋅ ℱ { ग्रॅम }

ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )

ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )

ℱ { एफ ( एन ) ⋅ जी ( एन )} = ℱ { एफ ( एन )} * ℱ { जी ( एन ) F = एफ ( के ) * जी ( के )

ℱ { एफ ( एन ) * जी ( एन )} = ℱ { एफ ( एन )} ⋅ ℱ { जी ( एन ) F = एफ ( के ) ⋅ जी ( के )

ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )

हे देखील पहा