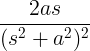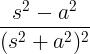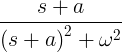लॅपलेस ट्रान्सफॉर्म

लॅपलेस शून्यापासून अनंतमध्ये समाकलित करून टाइम डोमेन फंक्शनला एस-डोमेन फंक्शनमध्ये रुपांतरित करते

वेळ डोमेन कार्याचे, ई- ^{गुणाद्वारे} गुणाकार .

लॅपलेस ट्रान्सफॉर्मचा उपयोग वेगळ्या समीकरणे आणि अविभाज्य द्रुतपणे निराकरण करण्यासाठी केला जातो.

टाईम डोमेनमधील व्युत्पत्ती एस-डोमेनमधील गुणामध्ये रुपांतरित केली जाते.

टाईम डोमेनमधील एकत्रीकरणाद्वारे एस-डोमेनमधील विभागणीत रूपांतरित होते.

लॅपलेस ट्रान्सफॉर्म फंक्शन

लॅप्लेस ट्रान्सफॉर्म एल lace {ऑपरेटरसह परिभाषित केले आहे :

$एफ (एस) = \ मॅथकॅल {एल} \ डावे \ {एफ (टी) \ राइट \} = \ इंट_ {०} ^ {\ इन्फ्टी} ई ^ {- एसटी} एफ (टी) दि.$

व्यस्त लॅपलेस ट्रान्सफॉर्मची गणना थेट केली जाऊ शकते.

सहसा ट्रान्सफॉर्म टेबलमधून व्यस्त ट्रान्सफॉर्म दिले जाते.

कार्य नाव	वेळ डोमेन कार्य	लॅपलेस ट्रान्सफॉर्म
कार्य नाव	फ ( टी )	फॅ ( एस ) = एल { एफ ( टी )}
सतत	1	$rac frac {1} {s}$
रेखीय	टी	$rac frac {1} {s ^ 2}$
शक्ती	टी ^एन	$rac frac {n!} {s ^ {n + 1}$
शक्ती	टी ^a	Γ ( a +1) ^-s ^{- ( a +1)}
घातांक	ई ^येथे	$rac frac {1} {sa}$
साईन	येथे पाप	$rac frac {a} {s ^ 2 + a ^ 2}$
कोझिन	कॉस येथे	$rac frac {s} {s ^ 2 + a ^ 2}$
हायपरबोलिक साइन	sinh at	$rac frac {a} {s ^ 2-a ^ 2}$
हायपरबोलिक कोसाइन	सोटा येथे	$rac frac {s} {s ^ 2-a ^ 2}$
वाढता साईन	टी येथे पाप	$rac frac {2as} {(s ^ 2 + a ^ 2) ^ 2$
वाढणारी कोसाइन	टी कॉस येथे	$rac frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2$
क्षय करणारा साईन	ई ^-ॅट पाप ωt	$rac frac {\ ओमेगा} {\ डावीकडे (s + a \ उजवीकडे) + 2 + \ ओमेगा ^ 2}$
क्षय कोसाइन	ई ^-at cos ωt	$rac frac {s + a} {\ डावीकडे (s + a \ उजवीकडे) + 2 + \ ओमेगा ^ 2}$
डेल्टा फंक्शन	t ( टी )	1
विलंबित डेल्टा	δ ( टा )	e ^-as

मालमत्तेचे नाव	वेळ डोमेन कार्य	लॅपलेस ट्रान्सफॉर्म	टिप्पणी
	फ ( टी )	फॅ ( एस )
रेषात्मकता	एएफ ( टी ) + बीजी ( टी )	AF ( s ) + बीजी ( s )	अ , ब स्थिर आहेत
स्केल बदल	f ( at )	$rac frac {1} {a} F \ डावीकडे (\ frac {s} {a} \ उजवीकडे)$	a / 0
शिफ्ट	e ^-at f ( t )	फॅ ( एस + ए )
विलंब	फ ( टा )	ई ^{- म्हणून} फॅ ( s )
व्युत्पन्न	$rac frac {df (t) {{dt$	एसएफ ( एस ) - एफ (0)
एन-व्या व्युत्पन्न	$rac frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
शक्ती	टी ^एन एफ ( टी )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
एकत्रीकरण	$\ int_ {0} ^ {t} f (x) dx$	$rac frac {1} {s} F (s)$
परस्पर	$rac frac {1} {t} f (t)$	$\ इंट_ {एस} ^ {\ इन्फ्टी} एफ (एक्स) डीएक्स$
कन्व्होल्यूशन	f ( t ) * g ( t )	फॅ ( एस ) ⋅ जी ( एस )	* हे कॉन्व्होल्यूशन ऑपरेटर आहे
नियतकालिक कार्य	f ( t ) = f ( t + T )	$rac frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$