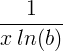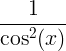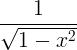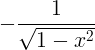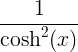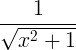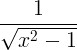व्युत्पन्न नियम
व्युत्पन्न नियम आणि कायदे. फंक्शन्स टेबलचे डेरिव्हेटिव्ह्ज.
व्युत्पन्न व्याख्या
फंक्शनचे व्युत्पन्न हे बिंदू x + Δx आणि x सह xx सह फंक्शन व्हॅल्यू एफ (एक्स) च्या फरकचे गुणोत्तर असते, जेव्हा infx अनंतच लहान असते. व्युत्पन्न बिंदू x वरील टेंगेंट लाइनचा फंक्शन उतार किंवा उतार आहे.
![]()
द्वितीय व्युत्पन्न
द्वितीय व्युत्पन्न दिले आहेः
![]()
किंवा फक्त प्रथम व्युत्पन्न:
![]()
Nth व्युत्पन्न
N व्या साधित f (x) एन वेळा असत करून गणना केली जाते.
N व्या भैदिज आहे (n-1) साधित व्युत्पन्न तुलना:
f ( n ) ( x ) = [ f ( n -1) ( x )] '
उदाहरणः
चा चौथा व्युत्पन्न शोधा
f ( x ) = 2 x 5
f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x
फंक्शनच्या आलेखावर व्युत्पन्न
फंक्शनचे व्युत्पन्न म्हणजे स्पर्शिका रेषाचा उतार.
व्युत्पन्न नियम
| व्युत्पन्न योग नियम | ( एएफ ( एक्स ) + बीजी ( एक्स )) '= एफ' ( एक्स ) + बीजी ' ( एक्स ) |
| व्युत्पन्न उत्पादनाचा नियम | ( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x ) |
| व्युत्पन्न भागांचा नियम | 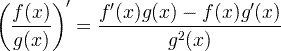 |
| व्युत्पन्न साखळी नियम | f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x ) |
व्युत्पन्न योग नियम
जेव्हा अ आणि ब स्थिर असतात.
( एएफ ( एक्स ) + बीजी ( एक्स )) '= एफ' ( एक्स ) + बीजी ' ( एक्स )
उदाहरणः
चे व्युत्पन्न शोधा:
3 x 2 + 4 x
बेरीज नियमानुसारः
a = 3, बी = 4
f ( x ) = x 2 , g ( x ) = x
f ' ( x ) = 2 x , g' ( x ) = 1
(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4
व्युत्पन्न उत्पादनाचा नियम
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
व्युत्पन्न भागांचा नियम
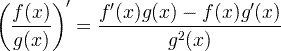
व्युत्पन्न साखळी नियम
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )
हा नियम लाग्रेंजच्या नोटेशनसह अधिक चांगल्या प्रकारे समजू शकतो:
![]()
फंक्शन रेषीय अंदाजे
लहान Δx साठी, आम्हाला f (x 0 + Δx) चे जवळपास मिळू शकते , जेव्हा आपल्याला f (x 0 ) आणि f '(x 0 ) माहित असते :
f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x
फंक्शन्स टेबलचे डेरिव्हेटिव्ह्ज
| कार्य नाव | कार्य | व्युत्पन्न |
|---|---|---|
| f ( x ) |
f '( x ) | |
| सतत | कॉन्स |
0 |
| रेखीय | x |
1 |
| शक्ती | x अ |
कुर्हाड a- 1 |
| घातांकीय | ई एक्स |
ई एक्स |
| घातांकीय | एक x |
एक एक्स एलएन ए |
| नैसर्गिक लॉगरिदम | एलएन ( एक्स ) |
|
| लोगारिदम | लॉग ब ( x ) |
|
| साईन | sin x |
कॉक्स एक्स |
| कोझिन | कॉक्स एक्स |
-सिन x |
| स्पर्शिका | टॅन एक्स |
|
| आर्केसिन | आर्क्सिन एक्स |
|
| आर्कोझिन | आर्ककोस एक्स |
|
| आर्क्टेंजंट | आर्कटान x |
|
| हायपरबोलिक साइन | sinh x |
कॉश एक्स |
| हायपरबोलिक कोसाइन | कॉश एक्स |
sinh x |
| हायपरबोलिक टॅन्जेन्ट | तान्ह x |
|
| व्यस्त हायपरबोलिक साइन | sinh -1 x |
|
| व्यस्त हायपरबोलिक कोसाइन | कोश -1 x |
|
| व्यस्त हायपरबोलिक स्पर्शिका | तान्ह -1 x |
|
व्युत्पन्न उदाहरणे
उदाहरण # 1
f ( x ) = x 3 +5 x 2 + x +8
f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1
उदाहरण # 2
f ( x ) = sin (3 x 2 )
साखळी नियम लागू करताना:
f ' ( x ) = कॉस (3 x 2 ) ⋅ [3 x 2 ]' = कॉस (3 x 2 ) ⋅ 6 x
दुसरी साधित चाचणी
जेव्हा कार्याचे प्रथम व्युत्पन्न बिंदू x 0 वर शून्य असते .
f '( x 0 ) = 0
तर बिंदू x 0 , f '' (x 0 ) वरील दुसरा व्युत्पन्न त्या बिंदूचा प्रकार दर्शवू शकतोः
| f '' ( x 0 )/ 0 |
स्थानिक किमान |
| f '' ( x 0 ) <0 |
स्थानिक कमाल |
| f '' ( x 0 ) = 0 |
निर्धारित |
हे देखील पहा
कॅल्कुलस
- मर्यादा
- व्युत्पन्न
- अखंड
- मालिका
- लॅपलेस ट्रान्सफॉर्म
- कन्व्होल्यूशन
- कॅल्क्युलस चिन्हे
वेगवान सारण्या