Taburan Kebarangkalian
Dalam kebarangkalian dan pengagihan statistik adalah ciri pemboleh ubah rawak, menerangkan kebarangkalian pemboleh ubah rawak dalam setiap nilai.
Setiap taburan mempunyai fungsi ketumpatan kebarangkalian dan fungsi taburan kebarangkalian.
Walaupun terdapat sebilangan besar pengagihan kebarangkalian, ada beberapa pengedaran biasa yang digunakan.
Fungsi pengagihan kumulatif
Taburan kebarangkalian dijelaskan oleh fungsi taburan kumulatif F (x),
yang merupakan kebarangkalian pemboleh ubah rawak X untuk mendapatkan nilai lebih kecil daripada atau sama dengan x:
F ( x ) = P ( X ≤ x )
Pengedaran berterusan
Fungsi taburan kumulatif F (x) dikira dengan penyatuan fungsi ketumpatan kebarangkalian f (u) pemboleh ubah rawak berterusan X.
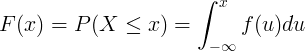
Pembahagian diskrit
Fungsi taburan kumulatif F (x) dikira dengan penjumlahan fungsi jisim kebarangkalian P (u) pemboleh ubah rawak diskrit X.
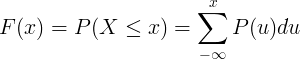
Jadual pengedaran berterusan
Pembahagian berterusan ialah pembahagian pemboleh ubah rawak berterusan.
Contoh pengedaran berterusan
...
Jadual pengedaran berterusan
| Nama pengedaran | Simbol pengedaran | Fungsi ketumpatan kebarangkalian (pdf) | Maksudnya | Varians |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| Biasa / gaussian | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| Pakaian seragam | X ~ U ( a , b ) |
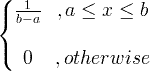 |
|
|
| Eksponensial | X ~ exp (λ) | |
|
|
| Gamma | X ~ gamma ( c , λ) | 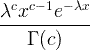 x / 0, c / 0, λ/ 0 |
|
|
| Chi Square | X ~ χ 2 ( k ) |
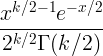 |
k |
2 k |
| Wishart | ||||
| F | X ~ F ( k 1 , k 2 ) |
|||
| Beta | ||||
| Weibull | ||||
| Log-normal | X ~ LN (μ, σ 2 ) |
|||
| Rayleigh | ||||
| Cauchy | ||||
| Dirichlet | ||||
| Laplace | ||||
| Pungutan | ||||
| Nasi | ||||
| Pelajar t |
Jadual pengedaran diskrit
Pembahagian diskrit adalah pembahagian pemboleh ubah rawak diskrit.
Contoh pembahagian diskrit
...
Jadual pengedaran diskrit
| Nama pengedaran | Simbol pengedaran | Fungsi jisim kebarangkalian (pmf) | Maksudnya | Varians | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| Binomial | X ~ Bin ( n , p ) |
|
np |
np (1- p ) |
|
| Poisson | X ~ Poisson (λ) |
|
λ ≥ 0 |
λ |
λ |
| Pakaian seragam | X ~ U ( a, b ) |
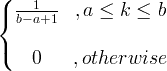 |
|
|
|
| Geometri | X ~ Geom ( hlm ) |
|
|
|
|
| Hyper-geometri | X ~ HG ( N , K , n ) |
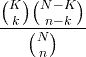 |
N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N |
|
|
| Bernoulli | X ~ Bern ( hlm ) |
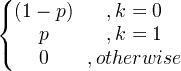 |
p |
p (1- p ) |
|
Lihat juga
KEBARANGKALIAN & STATISTIK
- Kebarangkalian asas
- Harapan
- Varians
- Sisihan piawai
- Taburan kebarangkalian
- Taburan normal
- Simbol statistik
JADUAL RAPID