Convolutie

Convolutie is de correlatiefunctie van f (τ) met de omgekeerde functie g (t-τ).

De convolutie-operator is het asterisk-symbool * .

De convolutie van f (t) en g (t) is gelijk aan de integraal van f (τ) maal f (t-τ):

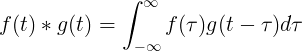
$f (t) * g (t) = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) d \ tau$

Convolutie van 2 discrete functies wordt gedefinieerd als:

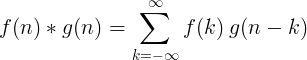
$f (n) * g (n) = \ sum_ {k = - \ infty} ^ {\ infty} f (k) \: g (nk)$

2-dimensionale discrete convolutie wordt meestal gebruikt voor beeldverwerking.

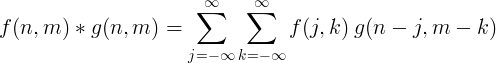
$f (n, m) * g (n, m) = \ sum_ {j = - \ infty} ^ {\ infty} \ sum_ {k = - \ infty} ^ {\ infty} f (j, k) \: g (nj, mk)$

We kunnen het discrete ingangssignaal x (n) filteren door convolutie met de impulsresponsie h (n) om het uitgangssignaal y (n) te krijgen.

y ( n ) = x ( n ) * h ( n )

De Fourier-transformatie van een vermenigvuldiging van 2 functies is gelijk aan de convolutie van de Fourier-transformaties van elke functie:

ℱ { f ⋅ g } = ℱ { f } * ℱ { g }

De Fourier-transformatie van een convolutie van 2 functies is gelijk aan de vermenigvuldiging van de Fourier-transformaties van elke functie:

ℱ { f * g } = ℱ { f } ⋅ ℱ { g }

ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )

ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )

ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )

ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )

ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )

Zie ook