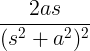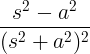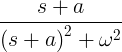Laplace-transformatie
- Laplace-transformatiefunctie
- Laplace-transformatietafel
- Laplace-transformatie-eigenschappen
- Laplace-transformatie voorbeelden
Laplace-transformatie converteert een tijddomeinfunctie naar een s-domeinfunctie door integratie van nul tot oneindig
van de tijddomeinfunctie, vermenigvuldigd met e -st .
De Laplace-transformatie wordt gebruikt om snel oplossingen te vinden voor differentiaalvergelijkingen en integralen.
Afleiding in het tijdsdomein wordt omgezet in vermenigvuldiging met s in het s-domein.
Integratie in het tijdsdomein wordt getransformeerd naar deling door s in het s-domein.
Laplace-transformatiefunctie
De Laplace-transformatie wordt gedefinieerd met de L {} - operator:
![]()
Inverse Laplace-transformatie
De inverse Laplace-transformatie kan direct worden berekend.
Gewoonlijk wordt de inverse transformatie gegeven vanuit de transformatietabel.
Laplace-transformatietafel
| Functienaam | Tijdsdomein functie | Laplace-transformatie |
|---|---|---|
f ( t ) |
F ( s ) = L { f ( t )} |
|
| Constante | 1 | |
| Lineair | t | |
| Kracht | t n |
|
| Kracht | t een |
Γ ( een +1) ⋅ s - ( een +1) |
| Exponent | e bij |
|
| Sinus | zonde bij |
|
| Cosinus | cos bij |
|
| Hyperbolische sinus | sinh bij |
|
| Hyperbolische cosinus | cosh op |
|
| Groeiende sinus | t zonde bij |
|
| Groeiende cosinus | t cos bij |
|
| Rottende sinus | e -at sin ωt |
|
| Afnemende cosinus | e -at cos ωt |
|
| Delta-functie | δ ( t ) |
1 |
| Vertraagde delta | δ ( ta ) |
e -as |
Laplace-transformatie-eigenschappen
| Eigendomsnaam | Tijdsdomein functie | Laplace-transformatie | Commentaar |
|---|---|---|---|
f ( t ) |
F ( s ) |
||
| Lineariteit | af ( t ) + bg ( t ) | aF ( s ) + bG ( s ) | a , b zijn constant |
| Schaalverandering | f ( bij ) | |
een / 0 |
| Verschuiving | e -at f ( t ) | F ( s + a ) | |
| Vertraging | f ( ta ) | e - als F ( s ) | |
| Afleiding | |
sF ( s ) - f (0) | |
| N-de afleiding | |
s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0) | |
| Kracht | t n f ( t ) | |
|
| Integratie | |
|
|
| Wederzijds | |
|
|
| Convolutie | f ( t ) * g ( t ) | F ( s ) ⋅ G ( s ) | * is de convolutie-operator |
| Periodieke functie | f ( t ) = f ( t + T ) | |
Laplace-transformatie voorbeelden
Voorbeeld 1
Vind de transformatie van f (t):
f ( t ) = 3 t + 2 t 2
Oplossing:
ℒ { t } = 1 / s 2
ℒ { t 2 } = 2 / s 3
F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3
Voorbeeld 2
Zoek de inverse transformatie van F (s):
F ( s ) = 3 / ( s 2 + s - 6)
Oplossing:
Om de inverse transformatie te vinden, moeten we de s-domeinfunctie wijzigen in een eenvoudiger vorm:
F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)
[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]
een ( s +3) + b ( s -2) = 3
Om a en b te vinden, krijgen we 2 vergelijkingen - een van de s-coëfficiënten en de tweede van de rest:
( a + b ) s + 3 een -2 b = 3
a + b = 0, 3 een -2 b = 3
a = 3/5, b = -3/5
F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)
Nu kunnen F (s) eenvoudig worden getransformeerd door de transformatietabel te gebruiken voor de exponentfunctie:
f ( t ) = (3/5) e 2 t - (3/5) e -3 t
Zie ook
CALCULUS
- Begrenzing
- Derivaat
- Integraal
- Serie
- Laplace-transformatie
- Convolutie
- Calculus symbolen
SNELLE TABELLEN