Arcsine-functie
arcsin (x), sin -1 (x), inverse sinusfunctie .
Arcsin-definitie
De arcsinus van x wordt gedefinieerd als de inverse sinusfunctie van x wanneer -1≤x≤1.
Als de sinus van y gelijk is aan x:
zonde y = x
Dan is de arcsinus van x gelijk aan de inverse sinusfunctie van x, die gelijk is aan y:
arcsin x = sin -1 x = y
Voorbeeld
arcsin 1 = sin -1 1 = π / 2 rad = 90 °
Grafiek van arcsin
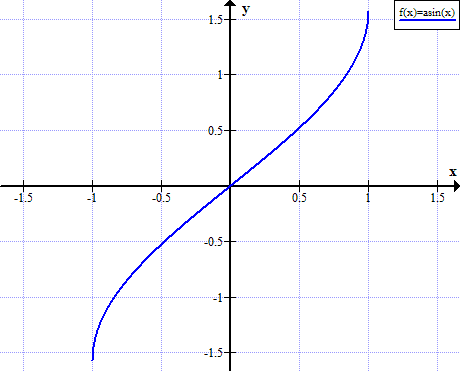
Arcsin regels
| Regelnaam | Regel |
|---|---|
| Sinus van bogen | sin (arcsin x ) = x |
| Arcsinus van sinus | arcsin (sin x ) = x +2 k π, wanneer k ∈ℤ ( k is een geheel getal) |
| Arcsin van negatief argument | arcsin (- x ) = - arcsin x |
| Complementaire hoeken | arcsin x = π / 2 - arccos x = 90 ° - arccos x |
| Arcsin som | arcsin α + arcsin ( β ) = arcsin ( α√ (1- β 2 ) + β√ (1- α 2 ) ) |
| Arcsin verschil | arcsin α - arcsin ( β ) = arcsin ( α√ (1- β 2 ) - β√ (1- α 2 ) ) |
| Cosinus van arcsinus | |
| Raaklijn van arcsinus | |
| Afgeleide van arcsinus | 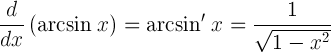 |
| Onbepaalde integraal van arcsinus |
Arcsin tafel
| x | arcsin (x) (rad) |
arcsin (x) (°) |
|---|---|---|
| -1 | -π / 2 | -90 ° |
| -√ 3 /2 | -π / 3 | -60 ° |
| -√ 2 /2 | -π / 4 | -45 ° |
| -1/2 | -π / 6 | -30 ° |
| 0 | 0 | 0 ° |
| 1/2 | π / 6 | 30 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 3 | 60 ° |
| 1 | π / 2 | 90 ° |
Zie ook
- Sinus functie
- Arccosine-functie
- Arctan-functie
- Arcsin rekenmachine
- Graden naar radialen converter
- Arcsin van 0
- Arcsin van 1
- Arcsin van oneindigheid
- Arcsin-grafiek
- Arcsin-derivaat
- Arcsin integraal
- Zonde van arcsin
- Cos van arcsin
- Tan van arcsin