Konvolusjon
Konvolusjon er korrelasjonsfunksjonen til f (τ) med den reverserte funksjonen g (t-τ).
Konvolusjonsoperatøren er stjernesymbolet * .
- Kontinuerlig konvolusjon
- Diskret konvolusjon
- 2D diskret konvolusjon
- Filtrer implementering med konvolusjon
- Konvolusjonssats
Kontinuerlig konvolusjon
Konvolusjonen av f (t) og g (t) er lik integralen av f (τ) ganger f (t-τ):
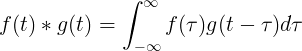
Diskret konvolusjon
Konvolusjon av to separate funksjoner er definert som:
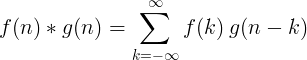
2D diskret konvolusjon
2-dimensjonal diskret konvolusjon brukes vanligvis til bildebehandling.
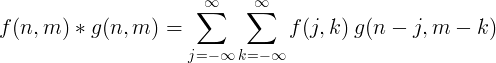
Filtrer implementering med konvolusjon
Vi kan filtrere det diskrete inngangssignalet x (n) ved konvolusjon med impulsresponsen h (n) for å få utgangssignalet y (n).
y ( n ) = x ( n ) * h ( n )
Konvolusjonssats
Fourier-transformasjonen av en multiplikasjon av to funksjoner er lik konvolusjonen av Fourier-transformasjonene av hver funksjon:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
Fourier-transformasjonen av en konvolusjon av to funksjoner er lik multiplikasjonen av Fourier-transformasjonene av hver funksjon:
ℱ { f * g } = ℱ { f } ⋅ ℱ { g }
Konvolusjonssetning for kontinuerlig Fourier-transformasjon
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
Konvolusjonssetning for diskret Fourier-transformasjon
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
Konvolusjonssetning for Laplace-transform
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )