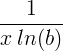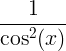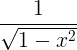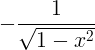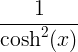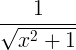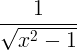Derivateregler
Avledede regler og lover. Derivater av funksjonstabellen.
Derivatdefinisjon
Derivatet til en funksjon er forholdet mellom forskjellen i funksjonsverdi f (x) i punktene x + Δx og x med Δx, når Δx er uendelig liten. Derivatet er funksjonshellingen eller hellingen til tangentlinjen ved punkt x.
![]()
Andre derivat
Det andre derivatet er gitt av:
![]()
Eller bare avled det første derivatet:
![]()
Nte derivat
Den n- te deriverte beregnes ved å utlede f (x) n ganger.
De n th derivatet er lik den deriverte av (n-1) derivatet:
f ( n ) ( x ) = [ f ( n -1) ( x )] '
Eksempel:
Finn det fjerde derivatet av
f ( x ) = 2 x 5
f (4) ( x ) = [2 x 5 ] '' '' [10 x 4 ] '' = [40 x 3 ] '' = [120 x 2 ] '= 240 x
Avledet på funksjonsgraf
Den avledede av en funksjon er skråningen av den tangentielle linjen.
Derivateregler
| Derivat sum regel | ( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x ) |
| Derivatproduktregel | ( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x ) |
| Derivatkvotientregel | 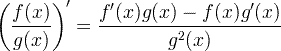 |
| Derivat kjederegel | f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x ) |
Derivat sum regel
Når a og b er konstanter.
( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Eksempel:
Finn derivatet av:
3 x 2 + 4 x.
I følge sumregelen:
a = 3, b = 4
f ( x ) = x 2 , g ( x ) = x
f ' ( x ) = 2 x , g' ( x ) = 1
(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4
Derivatproduktregel
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Derivatkvotientregel
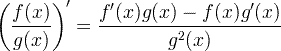
Derivat kjederegel
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )
Denne regelen kan forstås bedre med Lagranges notasjon:
![]()
Funksjon lineær tilnærming
For liten Δx kan vi få en tilnærming til f (x 0 + Δx), når vi vet f (x 0 ) og f '(x 0 ):
f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x
Derivater av funksjonstabellen
| Funksjonsnavn | Funksjon | Derivat |
|---|---|---|
| f ( x ) |
f '( x ) | |
| Konstant | konst |
0 |
| Lineær | x |
1 |
| Makt | x a |
øks a- 1 |
| Eksponentiell | e x |
e x |
| Eksponentiell | a x |
a x ln a |
| Naturlig logaritme | ln ( x ) |
|
| Logaritme | logg b ( x ) |
|
| Sine | synd x |
cos x |
| Cosine | cos x |
-sin x |
| Tangent | tan x |
|
| Arcsine | bueskinn x |
|
| Arccosine | arccos x |
|
| Arktangent | arctan x |
|
| Hyperbolisk sinus | sinh x |
koselig x |
| Hyperbolisk cosinus | koselig x |
sinh x |
| Hyperbolisk tangens | tanh x |
|
| Invers hyperbolsk sinus | sinh -1 x |
|
| Invers hyperbolsk cosinus | cosh -1 x |
|
| Invers hyperbolsk tangens | tanh -1 x |
|
Derivative eksempler
Eksempel 1
f ( x ) = x 3 +5 x 2 + x +8
f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1
Eksempel 2
f ( x ) = sin (3 x 2 )
Når du bruker kjederegelen:
f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x
Andre derivat test
Når det første derivatet av en funksjon er null ved punktet x 0 .
f '( x 0 ) = 0
Deretter kan det andre derivatet ved punkt x 0 , f '' (x 0 ), indikere typen for det punktet:
| f '' ( x 0 )/ 0 |
lokalt minimum |
| f '' ( x 0 ) <0 |
lokalt maksimum |
| f '' ( x 0 ) = 0 |
ubestemt |