Standardavvik

I sannsynlighet og statistikk er standardavviket til en tilfeldig variabel den gjennomsnittlige avstanden til en tilfeldig variabel fra gjennomsnittsverdien.

Den representerer hvordan den tilfeldige variabelen fordeles nær middelverdien. Lite standardavvik indikerer at den tilfeldige variabelen er fordelt nær middelverdien. Stort standardavvik indikerer at den tilfeldige variabelen er distribuert langt fra middelverdien.

Standardavvik definisjonsformel

Standardavviket er kvadratroten til variansen til tilfeldig variabel X, med gjennomsnittsverdien på μ.

\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

Fra definisjonen av standardavviket vi kan få

\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Standardavvik for kontinuerlig tilfeldig variabel

For kontinuerlig tilfeldig variabel med gjennomsnittsverdi μ og sannsynlighetstetthetsfunksjon f (x):

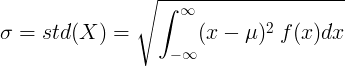
\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

eller

\ sigma = std (X) = \ sqrt {\ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}

Standardavvik for diskret tilfeldig variabel

For diskret tilfeldig variabel X med middelverdi μ og sannsynlighetsmassefunksjon P (x):

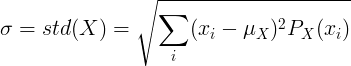
\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

eller

\ sigma = std (X) = \ sqrt {\ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2}

 

Sannsynlighetsfordeling ►

 

Se også

SANNLIKHET & STATISTIKK
RAPID BORD