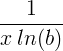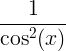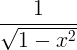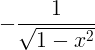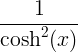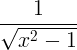Reguły pochodne
Pochodne reguły i prawa. Pochodne tabeli funkcji.
Definicja pochodna
Pochodna funkcji jest stosunkiem różnicy wartości funkcji f (x) w punktach x + Δx ix z Δx, gdy Δx jest nieskończenie mała. Pochodna jest funkcją nachylenia lub nachylenia stycznej w punkcie x.
![]()
Druga pochodna
Drugą pochodną jest:
![]()
Lub po prostu wyprowadź pierwszą pochodną:
![]()
N-ta pochodna
N p pochodnej jest obliczana poprzez wyprowadzenie F (x) n razy.
Gdy n TH pochodne równej pochodna (n-1), pochodną:
f ( n ) ( x ) = [ f ( n -1) ( x )] ”
Przykład:
Znajdź czwartą pochodną funkcji
f ( x ) = 2 x 5
f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x
Pochodna na wykresie funkcji
Pochodną funkcji jest nachylenie linii stycznej.
Reguły pochodne
| Reguła sum pochodnych | ( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x ) |
| Reguła iloczynu pochodnego | ( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x ) |
| Reguła pochodna ilorazu | 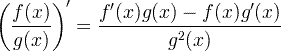 |
| Reguła łańcucha pochodnego | f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x ) |
Reguła sum pochodnych
Gdy a i b są stałymi.
( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Przykład:
Znajdź pochodną:
3 x 2 + 4 x.
Zgodnie z zasadą sumy:
a = 3, b = 4
f ( x ) = x 2 , g ( x ) = x
f ' ( x ) = 2 x , g' ( x ) = 1
(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4
Reguła iloczynu pochodnego
( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Reguła pochodna ilorazu
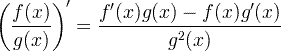
Reguła łańcucha pochodnego
f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )
Tę regułę można lepiej zrozumieć za pomocą notacji Lagrange'a:
![]()
Aproksymacja liniowa funkcji
Dla małego Δx możemy uzyskać przybliżenie do f (x 0 + Δx), gdy znamy f (x 0 ) if '(x 0 ):
f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x
Pochodne tabeli funkcji
| Nazwa funkcji | Funkcjonować | Pochodna |
|---|---|---|
| f ( x ) |
f '( x ) | |
| Stały | konst |
0 |
| Liniowy | x |
1 |
| Moc | x a |
topór a- 1 |
| Wykładniczy | e x |
e x |
| Wykładniczy | a x |
a x ln a |
| Naturalny logarytm | ln ( x ) |
|
| Logarytm | log b ( x ) |
|
| Sinus | sin x |
cos x |
| Cosinus | cos x |
-sin x |
| Tangens | tan x |
|
| Arcsine | arcsin x |
|
| Arccosine | arccos x |
|
| Arctangent | arctan x |
|
| Sinus hiperboliczny | sinh x |
cosh x |
| Cosinus hiperboliczny | cosh x |
sinh x |
| Styczna hiperboliczna | tanh x |
|
| Odwrotny sinus hiperboliczny | sinh -1 x |
|
| Odwrotny cosinus hiperboliczny | cosh -1 x |
|
| Odwrotna styczna hiperboliczna | tanh -1 x |
|
Pochodne przykłady
Przykład 1
f ( x ) = x 3 +5 x 2 + x +8
f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1
Przykład nr 2
f ( x ) = sin (3 x 2 )
Stosując regułę łańcucha:
f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x
Test drugiej pochodnej
Gdy pierwsza pochodna funkcji wynosi zero w punkcie x 0 .
f '( x 0 ) = 0
Wtedy druga pochodna w punkcie x 0 , f '' (x 0 ), może wskazywać na typ tego punktu:
| f '' ( x 0 )/ 0 |
minimum lokalne |
| f '' ( x 0 ) <0 |
lokalne maksimum |
| f '' ( x 0 ) = 0 |
nieokreślony |
Zobacz też
RACHUNEK RÓŻNICZKOWY
- Limit
- Pochodna
- Całka
- Seria
- Transformata Laplace'a
- Skręt
- Symbole rachunku różniczkowego
SZYBKIE STOŁY