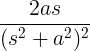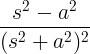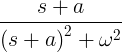Transformata Laplace'a
- Funkcja transformaty Laplace'a
- Tabela transformacji Laplace'a
- Właściwości transformaty Laplace'a
- Przykłady transformacji Laplace'a
Transformata Laplace'a konwertuje funkcję w dziedzinie czasu na funkcję w dziedzinie s przez całkowanie od zera do nieskończoności
funkcji w dziedzinie czasu pomnożonej przez e- st .
Transformata Laplace'a służy do szybkiego znajdowania rozwiązań równań różniczkowych i całek.
Wyprowadzenie w dziedzinie czasu przekształca się w pomnożenie przez sw dziedzinie s.
Całkowanie w dziedzinie czasu jest przekształcane w dzielenie przez s w dziedzinie s.
Funkcja transformaty Laplace'a
Transformatę Laplace'a definiuje się za pomocą operatora L {}:
![]()
Odwrotna transformata Laplace'a
Odwrotną transformatę Laplace'a można obliczyć bezpośrednio.
Zwykle transformacja odwrotna jest podawana z tabeli przekształceń.
Tabela transformacji Laplace'a
| Nazwa funkcji | Funkcja w dziedzinie czasu | Transformata Laplace'a |
|---|---|---|
f ( t ) |
F ( s ) = L { f ( t )} |
|
| Stały | 1 | |
| Liniowy | t | |
| Moc | t n |
|
| Moc | t a |
Γ ( a +1) ⋅ s - ( a +1) |
| Wykładnik potęgowy | e w |
|
| Sinus | grzech w |
|
| Cosinus | cos w |
|
| Sinus hiperboliczny | sinh at |
|
| Cosinus hiperboliczny | cosh w |
|
| Rosnący sinus | t sin w |
|
| Rosnący cosinus | t cos w |
|
| Rozkładający się sinus | e -w sin ωt |
|
| Rozkładający się cosinus | e -w cos ωt |
|
| Funkcja delta | δ ( t ) |
1 |
| Delta opóźniona | δ ( ta ) |
e -as |
Właściwości transformaty Laplace'a
| Nazwa właściwości | Funkcja w dziedzinie czasu | Transformata Laplace'a | Komentarz |
|---|---|---|---|
f ( t ) |
F ( s ) |
||
| Liniowość | af ( t ) + bg ( t ) | aF ( s ) + bG ( s ) | a , b są stałe |
| Zmiana skali | f ( małpa ) | |
a / 0 |
| Zmiana | e -at f ( t ) | F ( s + a ) | |
| Opóźnienie | f ( ta ) | e - jak F ( s ) | |
| Pochodzenie | |
sF ( s ) - f (0) | |
| N-ta wyprowadzenie | |
s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0) | |
| Moc | t n f ( t ) | |
|
| Integracja | |
|
|
| Odwrotność | |
|
|
| Skręt | f ( t ) * g ( t ) | F ( s ) ⋅ G ( s ) | * jest operatorem splotu |
| Funkcja okresowa | f ( t ) = f ( t + T ) | |
Przykłady transformacji Laplace'a
Przykład 1
Znajdź transformację f (t):
f ( t ) = 3 t + 2 t 2
Rozwiązanie:
ℒ { t } = 1 / s 2
ℒ { t 2 } = 2 / s 3
F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3
Przykład nr 2
Znajdź odwrotną transformację F (s):
F ( s ) = 3 / ( s 2 + s - 6)
Rozwiązanie:
Aby znaleźć transformację odwrotną, musimy zmienić funkcję domeny s na prostszą postać:
F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)
[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]
a ( s +3) + b ( s -2) = 3
Aby znaleźć a i b, otrzymujemy 2 równania - jeden ze współczynników s i drugi z pozostałych:
( a + b ) s + 3 a -2 b = 3
a + b = 0, 3 a -2 b = 3
a = 3/5, b = -3/5
F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)
Teraz F (s) można łatwo przekształcić, używając tabeli przekształceń dla funkcji wykładniczej:
f ( t ) = (3/5) e 2 t - (3/5) e -3 t
Zobacz też
RACHUNEK RÓŻNICZKOWY
- Limit
- Pochodna
- Całka
- Seria
- Transformata Laplace'a
- Skręt
- Symbole rachunku różniczkowego
SZYBKIE STOŁY