Integrante

Integração é a operação reversa de derivação.

O Integral de uma função é a área sob o gráfico da função.

Definição Integral Indefinida

Quando dF (x) / dx = f (x) =/ integral (f (x) * dx) = F (x) + c

Propriedades Integrais Indefinidas

integral (f (x) + g (x)) * dx = integral (f (x) * dx) + integral (g (x) * dx)

integral (a * f (x) * dx) = a * integral (f (x) * dx)

integral (f (a * x) * dx) = 1 / a * F (a * x) + c

integral (f (x + b) * dx) = F (x + b) + c

integral (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

integral (df (x) / dx * dx) = f (x)

Mudança de Variável de Integração

Quandox = g (t) edx = g '(t) * dt

integral (f (x) * dx) = integral (f (g (t)) * g '(t) * dt)

Integração por partes

integral (f (x) * g '(x) * dx) = f (x) * g (x) - integral (f' (x) * g (x) * dx)

Tabela de Integrais

integral (f (x) * dx = F (x) + c

integral (a * dx) = a * x + c

integral (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, quando a </ - 1

integral (1 / x * dx) = ln (abs (x)) + c

integral (e ^ x * dx) = e ^ x + c

integral (a ^ x * dx) = a ^ x / ln (x) + c

integral (ln (x) * dx) = x * ln (x) - x + c

integral (sin (x) * dx) = -cos (x) + c

integral (cos (x) * dx) = sin (x) + c

integral (tan (x) * dx) = -ln (abs (cos (x))) + c

integral (arcsin (x) * dx) = x * arcsin (x) + sqrt (1-x ^ 2) + c

integral (arccos (x) * dx) = x * arccos (x) - sqrt (1-x ^ 2) + c

integral (arctan (x) * dx) = x * arctan (x) - 1/2 * ln (1 + x ^ 2) + c

integral (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

integral (1 / sqrt (a ^ 2-x ^ 2) * dx) = arcsin (x / a) + c

integral (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

integral (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

integral (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * arctan (x / a) + c

integral (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

integral (sinh (x) * dx) = cosh (x) + c

integral (cosh (x) * dx) = sinh (x) + c

integral (tanh (x) * dx) = ln (cosh (x)) + c

 

Definição Integral Definida

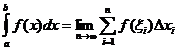
integral (a..b, f (x) * dx) = lim (n-/ inf, soma (i = 1..n, f (z (i)) * dx (i))) 

Quandox0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

Cálculo Integral Definido

Quando ,

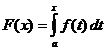 dF (x) / dx = f (x) e

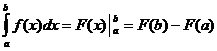
integral (a..b, f (x) * dx) = F (b) - F (a) 

Propriedades Integrais Definidas

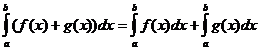
integral (a..b, (f (x) + g (x)) * dx) = integral (a..b, f (x) * dx) + integral (a..b, g (x) * dx )

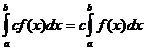
integral (a..b, c * f (x) * dx) = c * integral (a..b, f (x) * dx)

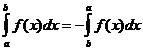
integral (a..b, f (x) * dx) = - integral (b..a, f (x) * dx)

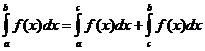
integral (a..b, f (x) * dx) = integral (a..c, f (x) * dx) + integral (c..b, f (x) * dx)

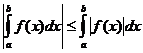
abs (integral (a..b, f (x) * dx)) <= integral (a..b, abs (f (x)) * dx)

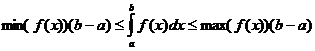min (f (x)) * (ba) <= integral (a..b, f (x) * dx) <= max (f (x)) * (ba) quandox membro de [a, b]

Mudança de Variável de Integração

Quandox = g (t) ,dx = g '(t) * dt ,g (alfa) = a ,g (beta) = b

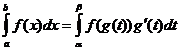
integral (a..b, f (x) * dx) = integral (alfa..beta, f (g (t)) * g '(t) * dt)

Integração por partes

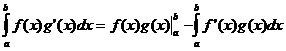
integral (a..b, f (x) * g '(x) * dx) = integral (a..b, f (x) * g (x) * dx) - integral (a..b, f' (x) * g (x) * dx)

Teorema do valor médio

Quando f ( x ) é contínuo, há um pontoc é membro de [a, b] tão

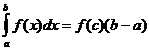
integral (a..b, f (x) * dx) = f (c) * (ba)  

Aproximação trapezoidal da integral definida

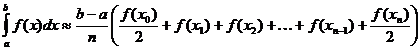
integral (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

A Função Gama

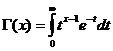
gama (x) = integral (0..inf, t ^ (x-1) * e ^ (- t) * dt

A função Gamma é convergente para x/ 0 .

Propriedades da função gama

G ( x +1) = x G ( x )

G ( n +1) = n ! , quando n ℕ (número inteiro positivo).é membro de

A Função Beta

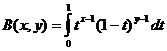
B (x, y) = integral (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

Função beta e relação da função gama

B (x, y) = Gamma (x) * Gamma (y) / Gamma (x + y)

 

 

 

CÁLCULO
TABELAS RÁPIDAS