Variância

Em probabilidade e estatística, a variância de uma variável aleatória é o valor médio da distância quadrada do valor médio. Ele representa como a variável aleatória é distribuída perto do valor médio. A pequena variância indica que a variável aleatória está distribuída perto do valor médio. Grande variância indica que a variável aleatória está distribuída longe do valor médio. Por exemplo, com distribuição normal, a curva em sino estreita terá pequena variância e a curva em sino ampla terá grande variação.

Definição de variância

A variância da variável aleatória X é o valor esperado dos quadrados da diferença de X e o valor esperado µ.

σ ² = Var ( X ) = E [( X - μ ) ² ]

A partir da definição da variação, podemos obter

σ ² = Var ( X ) = E ( X ² ) - μ ²

Variância da variável aleatória contínua

Para variável aleatória contínua com valor médio μ e função de densidade de probabilidade f (x):

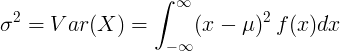
$\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx$

$Var (X) = \ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2$

Variância da variável aleatória discreta

Para variável aleatória discreta X com valor médio μ e função de massa de probabilidade P (x):

$\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)$

$Var (X) = \ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2$

Propriedades de variância

Quando X e Y são variáveis aleatórias independentes:

Var ( X + Y ) = Var ( X ) + Var ( Y )

Desvio padrão ►

Variância

Definição de variância

Variância da variável aleatória contínua

Variância da variável aleatória discreta

Propriedades de variância

Var ( X + Y ) = Var ( X ) + Var ( Y )

Veja também

PROBABILIDADE E ESTATÍSTICAS

TABELAS RÁPIDAS