Distribuição de probabilidade

Em probabilidade e distribuição estatística é uma característica de uma variável aleatória, descreve a probabilidade da variável aleatória em cada valor.

Cada distribuição tem uma certa função de densidade de probabilidade e função de distribuição de probabilidade.

Embora haja um número indefinido de distribuições de probabilidade, há várias distribuições comuns em uso.

Função de distribuição cumulativa

A distribuição de probabilidade é descrita pela função de distribuição cumulativa F (x),

que é a probabilidade da variável aleatória X obter um valor menor ou igual a x:

F ( x ) = P ( X ≤ x )

Distribuição contínua

A função de distribuição cumulativa F (x) é calculada pela integração da função de densidade de probabilidade f (u) da variável aleatória contínua X.

Distribuição discreta

A função de distribuição cumulativa F (x) é calculada pela soma da função de massa de probabilidade P (u) da variável aleatória discreta X.

Tabela de distribuição contínua

A distribuição contínua é a distribuição de uma variável aleatória contínua.

Exemplo de distribuição contínua

...

Tabela de distribuição contínua

Nome de distribuição Símbolo de distribuição Função de densidade de probabilidade (pdf) Significar Variância
   

f X ( x )

μ = E ( X )

σ 2 = Var ( X )
Normal / gaussiano

X ~ N (μ, σ 2 )

 \ frac {1} {\ sigma \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}} μ σ 2
Uniforme

X ~ U ( a , b )

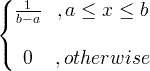 \ begin {Bmatrix} \ frac {1} {ba} &, a \ leq x \ leq b \\ & \\ 0 &, caso contrário, \ end {matrix} \ frac {(ba) ^ 2} {12}
Exponencial X ~ exp (λ) \ begin {Bmatrix} \ lambda e ^ {- \ lambda x} & x \ geq 0 \\ 0 & x <0 \ end {matrix} \ frac {1} {\ lambda} \ frac {1} {\ lambda ^ 2}
Gama X ~ gama ( c , λ) 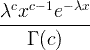\ frac {\ lambda ^ cx ^ {c-1} e ^ {- \ lambda x}} {\ Gamma (c)}

x / 0, c / 0, λ/ 0

 \ frac {c} {\ lambda} \ frac {c} {\ lambda ^ 2}
Chi quadrado

X ~ χ 2 ( k )

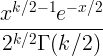 \ frac {x ^ {k / 2-1} e ^ {- x / 2}} {2 ^ {k / 2} \ Gamma (k / 2)}

k

2 mil
Wishart        
F

X ~ F ( k 1 , k 2 )

      
Beta        
Weibull        
Log normal

X ~ LN (μ, σ 2 )

      
Rayleigh        
Cauchy        
Dirichlet        
Laplace        
Imposição        
Arroz        
T de estudante        

Tabela de distribuição discreta

A distribuição discreta é a distribuição de uma variável aleatória discreta.

Exemplo de distribuição discreta

...

Tabela de distribuição discreta

Nome de distribuição Símbolo de distribuição Função de massa de probabilidade (pmf) Significar Variância
    f x ( k ) = P ( X = k )

k = 0,1,2, ...

 E ( x ) Var ( x )
Binomial

X ~ Bin ( n , p )

 \ binom {n} {k} p ^ {k} (1-p) ^ {nk}

np

np (1- p )
Poisson

X ~ Poisson (λ)

λ ≥ 0

λ

λ

Uniforme

X ~ U ( a, b )

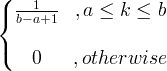 \ begin {Bmatrix} \ frac {1} {b-a + 1} &, a \ leq k \ leq b \\ & \\ 0 &, caso contrário, \ end {matrix} \ frac {a + b} {2} \ frac {(b-a + 1) ^ {2} -1} {12}
Geométrico

X ~ Geom ( p )

 p (1-p) ^ {k}

\ frac {1-p} {p}

\ frac {1-p} {p ^ 2}
Hiper-geométrica

X ~ HG ( N , K , n )

N = 0,1,2, ...

K = 0,1, .., N

n = 0,1, ..., N

 \ frac {nK} {N} \ frac {nK (NK) (Nn)} {N ^ 2 (N-1)}
Bernoulli

X ~ Bern ( p )

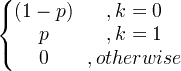 \ begin {Bmatrix} (1-p) &, k = 0 \\ p &, k = 1 \\ 0 &, caso contrário, \ end {matrix}

p

p (1- p )

 

Veja também

PROBABILIDADE E ESTATÍSTICAS
TABELAS RÁPIDAS