Convoluţie
Convoluția este funcția de corelație a lui f (τ) cu funcția inversată g (t-τ).
Operatorul de convoluție este simbolul asteriscului * .
- Convoluție continuă
- Convoluție discretă
- Convoluție discretă 2D
- Implementarea filtrului cu convoluție
- Teorema convoluției
Convoluție continuă
Convoluția lui f (t) și g (t) este egală cu integralul f (τ) ori f (t-τ):
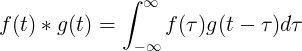
Convoluție discretă
Convoluția a 2 funcții discrete este definită ca:
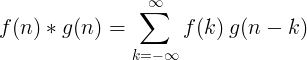
Convoluție discretă 2D
Convoluția discretă bidimensională este de obicei utilizată pentru procesarea imaginilor.
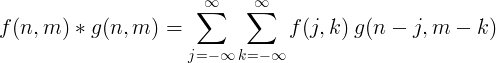
Implementarea filtrului cu convoluție
Putem filtra semnalul discret de intrare x (n) prin convoluție cu răspunsul la impuls h (n) pentru a obține semnalul de ieșire y (n).
y ( n ) = x ( n ) * h ( n )
Teorema convoluției
Transformata Fourier a unei multiplicări a 2 funcții este egală cu convoluția transformatelor Fourier ale fiecărei funcții:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
Transformata Fourier a unei convoluții a 2 funcții este egală cu înmulțirea transformatelor Fourier ale fiecărei funcții:
ℱ { f * g } = ℱ { f } ⋅ ℱ { g }
Teorema convoluției pentru transformată Fourier continuă
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
Teorema convoluției pentru transformată Fourier discretă
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
Teorema convoluției pentru transformata Laplace
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )
Vezi si
CALCUL
- Limită
- Derivat
- Integral
- Serie
- Transformarea Laplace
- Convoluţie
- Simboluri de calcul
MESE RAPIDE