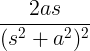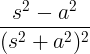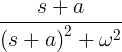Transformarea Laplace

Transformarea Laplace convertește o funcție de domeniu de timp în funcție de domeniu s prin integrare de la zero la infinit

a funcției domeniului timp, înmulțit cu e ^-st .

Transformata Laplace este utilizată pentru a găsi rapid soluții pentru ecuații diferențiale și integrale.

Derivarea în domeniul timpului este transformată în multiplicare cu s în domeniul s.

Integrarea în domeniul timpului este transformată în divizare cu s în domeniul s.

Funcția de transformare Laplace

Transformata Laplace este definită cu operatorul L {}:

$F (s) = \ mathcal {L} \ left \ {f (t) \ right \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

Transformata Laplace inversă poate fi calculată direct.

De obicei transformarea inversă este dată din tabelul de transformări.

Numele funcției	Funcția domeniului timp	Transformarea Laplace
Numele funcției	f ( t )	F ( s ) = L { f ( t )}
Constant	1	$\ frac {1} {s}$
Liniar	t	$\ frac {1} {s ^ 2}$
Putere	t ⁿ	$\ frac {n!} {s ^ {n + 1}}$
Putere	t ^a	Γ ( a +1) ⋅ s ^{- ( a +1)}
Exponent	e ^la	$\ frac {1} {sa}$
Sinus	păcatul la	$\ frac {a} {s ^ 2 + a ^ 2}$
Cosinus	cos at	$\ frac {s} {s ^ 2 + a ^ 2}$
Sinus hiperbolic	sinh at	$\ frac {a} {s ^ 2-a ^ 2}$
Cosinus hiperbolic	cosh la	$\ frac {s} {s ^ 2-a ^ 2}$
Sinus în creștere	t păcat la	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
Cosinus în creștere	t cos at	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
Sinus în descompunere	e ^-at sin ωt	$\ frac {\ omega} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
Cosinus în descompunere	e ^-at cos ωt	$\ frac {s + a} {\ left (s + a \ right) ^ 2 + \ omega ^ 2}$
Funcția Delta	δ ( t )	1
Delta întârziată	δ ( ta )	e ^-as

Numele proprietatii	Funcția domeniului timp	Transformarea Laplace	cometariu
	f ( t )	F ( e )
Liniaritatea	af ( t ) + bg ( t )	aF ( s ) + bG ( s )	a , b sunt constante
Schimbarea scalei	f ( la )	$\ frac {1} {a} F \ left (\ frac {s} {a} \ right)$	a / 0
Schimb	e ^-at f ( t )	F ( s + a )
Întârziere	f ( ta )	e ^{- ca} F ( e )
Derivare	$\ frac {df (t)} {dt}$	sF ( s ) - f (0)
Derivația a N-a	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
Putere	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
Integrare	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F (s)$
Reciproc	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
Convoluţie	f ( t ) * g ( t )	F ( s ) ⋅ G ( s )	* este operatorul de convoluție
Funcția periodică	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$