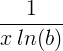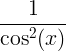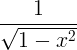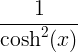Reguli derivate

Reguli și legi derivate. Derivatele tabelului de funcții.

Definiție derivată

Derivata unei funcții este raportul dintre diferența valorii funcției f (x) la punctele x + Δx și x cu Δx, când Δx este infinit de mic. Derivata este panta funcției sau panta liniei tangente la punctul x.

 

f '(x) = \ lim _ {\ Delta x \ to 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}

A doua derivată

A doua derivată este dată de:

Sau pur și simplu derivă primul derivat:

f '' (x) = (f '(x))'

Derivata a N-a

N th Derivatul este calculat prin derivarea f (x) n ori.

De n th derivă egal cu derivata (n-1) Derivatul:

f ( n ) ( x ) = [ f ( n -1) ( x )] '

Exemplu:

Găsiți a patra derivată a

f ( x ) = 2 x 5

f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x

Derivată pe graficul funcției

Derivata unei funcții este înclinarea liniei tangențiale.

Reguli derivate

Regula sumei derivate

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Regula produsului derivat

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Regula coeficientului derivat 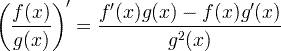\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( X)}
Regula lanțului derivat

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Regula sumei derivate

Când a și b sunt constante.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Exemplu:

Găsiți derivatul:

3 x 2 + 4 x.

Conform regulii de sumă:

a = 3, b = 4

f ( x ) = x 2 , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Regula produsului derivat

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Regula coeficientului derivat

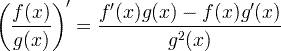
\ left (\ frac {f (x)} {g (x)} \ right) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( X)}

Regula lanțului derivat

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Această regulă poate fi mai bine înțeleasă cu notația Lagrange:

\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}

Funcție aproximare liniară

Pentru Δx mic, putem obține o aproximare la f (x 0 + Δx), când știm f (x 0 ) și f '(x 0 ):

f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x

Derivatele tabelului de funcții

Numele funcției Funcţie Derivat

f ( x )

 f '( x )
Constant

const

0

Liniar

x

1

Putere

x a

ax a- 1
Exponențială

e x

e x
Exponențială

un x

a x ln a
Logaritm natural

ln ( x )

Logaritm

jurnal b ( x )

Sinus

păcat x

cos x
Cosinus

cos x

-păcatul x
Tangentă

tan x

Arcsine

arcsin x

Arccosine

arccos x

Arctangent

arctan x
Sinus hiperbolic

sinh x

cosh x
Cosinus hiperbolic

cosh x

sinh x
Tangentă hiperbolică

tanh x

Sinus hiperbolic invers

sinh -1 x

Cosinus hiperbolic invers

cosh -1 x

Tangentă hiperbolică inversă

tanh -1 x

Exemple derivate

Exemplul nr. 1

f ( x ) = x 3 +5 x 2 + x +8

f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1

Exemplul nr. 2

f ( x ) = sin (3 x 2 )

Când aplicați regula lanțului:

f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x

Al doilea test derivat

Când prima derivată a unei funcții este zero la punctul x 0 .

f '( x 0 ) = 0

Apoi, a doua derivată la punctul x 0 , f "(x 0 ), poate indica tipul acelui punct:

 

f "( x 0 )/ 0

 minim local

f "( x 0 ) <0

 maxim local

f "( x 0 ) = 0

 nedeterminat

 

Vezi si

CALCUL
MESE RAPIDE