Квадратное уровненеие
Квадратное уравнение - это полином второго порядка с 3-мя коэффициентами - a , b , c .
Квадратичное уравнение задается следующим образом:
ах 2 + Ьх + с = 0
Решение квадратного уравнения дается двумя числами x 1 и x 2 .
Мы можем изменить квадратное уравнение к виду:
( х - х 1 ) ( х - х 2 ) = 0
Квадратичная формула
Решение квадратного уравнения дается квадратной формулой:
![]()
Выражение внутри квадратного корня называется дискриминантом и обозначается Δ:
Δ = b 2 - 4 переменного тока
Квадратичная формула с дискриминантными обозначениями:
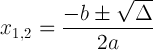
Это выражение важно, потому что оно может рассказать нам о решении:
- Когда Δ/ 0, есть 2 действительных корня x 1 = (- b + √ Δ ) / (2a) и x 2 = (- b-√ Δ ) / (2a) .
- Когда Δ = 0, имеется один корень x 1 = x 2 = -b / (2a) .
- Когда Δ <0, нет действительных корней, есть 2 комплексных корня:
x 1 = (- b + i√ -Δ ) / (2a) и x 2 = (- bi√ -Δ ) / (2a) .
Проблема # 1
3 х 2 +5 х +2 = 0
решение:
а = 3, б = 5, с = 2
х 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
х 1 = (-5 + 1) / 6 = -4/6 = -2/3
х 2 = (-5 - 1) / 6 = -6/6 = -1
Проблема # 2
3 х 2 -6 х + 3 = 0
решение:
а = 3, б = -6, в = 3
х 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
х 1 = х 2 = 1
Проблема # 3
х 2 +2 х +5 = 0
решение:
а = 1, б = 2, с = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Реальных решений нет. Значения представляют собой комплексные числа:
х 1 = -1 + 2 я
х 2 = -1 - 2 я
График квадратичных функций
Квадратичная функция - это полиномиальная функция второго порядка:
f ( x ) = ax 2 + bx + c
Решениями квадратного уравнения являются корни квадратичной функции, которые являются точками пересечения графика квадратичной функции с осью x, когда
f ( x ) = 0
Когда есть 2 точки пересечения графика с осью x, есть 2 решения квадратного уравнения.
Когда есть 1 точка пересечения графика с осью x, существует 1 решение квадратного уравнения.
Когда нет точек пересечения графика с осью x, мы получаем не реальные решения (или 2 комплексных решения).