Правила логарифмирования
База б логарифм ряда является показателем , что нам нужно , чтобы поднять базу для того , чтобы получить номер.
- Определение логарифма
- Правила логарифмирования
- Задачи логарифмирования
- Комплексный логарифм
- График log (x)
- Таблица логарифмов
- Калькулятор логарифмов
Определение логарифма
Когда b возведен в степень y, равен x:
б у = х
Тогда логарифм x по основанию b равен y:
журнал b ( x ) = y
Например, когда:
2 4 = 16
затем
журнал 2 (16) = 4
Логарифм как функция, обратная экспоненциальной функции
Логарифмическая функция,
у = журнал b ( х )
является функцией, обратной экспоненциальной функции,
х = б у
Итак, если мы вычислим экспоненциальную функцию логарифма x (x/ 0),
f ( f -1 ( x )) = b журнал b ( x ) = x
Или, если мы вычислим логарифм экспоненциальной функции x,
f -1 ( f ( x )) = журнал b ( b x ) = x
Натуральный логарифм (ln)
Натуральный логарифм - это логарифм по основанию е:
ln ( x ) = журнал e ( x )
Когда константа e - это число:
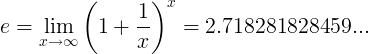
или
![]()
См .: Натуральный логарифм.
Расчет обратного логарифма
Обратный логарифм (или антилогарифм) вычисляется путем возведения основания b до логарифма y:
х = журнал -1 ( у ) = б у
Логарифмическая функция
Логарифмическая функция имеет базовую форму:
f ( x ) = журнал b ( x )
Правила логарифмирования
| Название правила | Правило |
|---|---|
Правило произведения логарифма |
журнал b ( x ∙ y ) = журнал b ( x ) + журнал b ( y ) |
Правило логарифмического отношения |
журнал b ( x / y ) = журнал b ( x ) - журнал b ( y ) |
Правило логарифма мощности |
журнал b ( x y ) = y ∙ log b ( x ) |
Правило переключения логарифма |
журнал b ( c ) = 1 / журнал c ( b ) |
Правило изменения основания логарифма |
журнал b ( x ) = журнал c ( x ) / журнал c ( b ) |
Производная логарифма |
f ( x ) = журнал b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b )) |
Интеграл от логарифма |
∫ журнал b ( x ) dx = x ∙ (журнал b ( x ) - 1 / ln ( b ) ) + C |
Логарифм отрицательного числа |
log b ( x ) не определено, когда x ≤ 0 |
Логарифм 0 |
log b (0) не определено |
Логарифм 1 |
журнал b (1) = 0 |
Логарифм основания |
журнал b ( b ) = 1 |
Логарифм бесконечности |
lim log b ( x ) = ∞, когда x → ∞ |
См .: Правила логарифмирования
Правило произведения логарифма
Логарифм умножения x и y - это сумма логарифма x и логарифма y.
журнал b ( x ∙ y ) = журнал b ( x ) + журнал b ( y )
Например:
журнал 10 (3 ∙ 7) = журнал 10 (3) + журнал 10 (7)
Правило логарифмического отношения
Логарифм деления x и y - это разность логарифма x и логарифма y.
журнал b ( x / y ) = журнал b ( x ) - журнал b ( y )
Например:
войти 10 (3 / 7) = войти 10 (3) - войти в 10 (7)
Правило логарифма мощности
Логарифм x в степени y равен y, умноженному на логарифм x.
журнал b ( x y ) = y ∙ log b ( x )
Например:
журнал 10 (2 8 ) = 8 ∙ журнал 10 (2)
Правило переключения логарифма
Логарифм c по основанию b равен 1, деленному на логарифм по основанию c числа b.
журнал b ( c ) = 1 / журнал c ( b )
Например:
журнал 2 (8) = 1 / журнал 8 (2)
Правило изменения основания логарифма
Логарифм x по основанию b равен основанию c логарифма x, деленному на логарифм b по основанию c.
журнал b ( x ) = журнал c ( x ) / журнал c ( b )
Например, чтобы вычислить лог 2 (8) в калькуляторе, нам нужно изменить базу на 10:
журнал 2 (8) = журнал 10 (8) / журнал 10 (2)
См .: правило изменения базы журнала
Логарифм отрицательного числа
Действительный логарифм по основанию b от x, когда x <= 0, не определен, когда x отрицателен или равен нулю:
log b ( x ) не определено, когда x ≤ 0
См .: журнал отрицательного числа
Логарифм 0
Логарифм нуля по основанию b не определен:
log b (0) не определено
Предел логарифма x по основанию b, когда x стремится к нулю, равен минус бесконечности:
![]()
Смотрите: журнал нуля
Логарифм 1
Логарифм единицы по основанию b равен нулю:
журнал b (1) = 0
Например, логарифм единицы по основанию два равен нулю:
журнал 2 (1) = 0
Смотрите: журнал одного
Логарифм бесконечности
Предел логарифма x по основанию b, когда x стремится к бесконечности, равен бесконечности:
lim log b ( x ) = ∞, когда x → ∞
Смотрите: журнал бесконечности
Логарифм основания
Базовый логарифм b равен единице:
журнал b ( b ) = 1
Например, логарифм двух по основанию два равен единице:
журнал 2 (2) = 1
Производная логарифма
когда
f ( x ) = журнал b ( x )
Тогда производная от f (x):
f ' ( x ) = 1 / ( x ln ( b ))
Смотрите: производная журнала
Логарифм интеграл
Интеграл от логарифма x:
∫ журнал b ( x ) dx = x ∙ (журнал b ( x ) - 1 / ln ( b ) ) + C
Например:
∫ журнал 2 ( x ) dx = x ∙ (журнал 2 ( x ) - 1 / ln (2) ) + C
Приближение логарифма
log 2 ( x ) ≈ n + ( x / 2 n - 1),
Комплексный логарифм
Для комплексного числа z:
z = re iθ = x + iy
Комплексный логарифм будет (n = ...- 2, -1,0,1,2, ...):
Журнал z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
Логарифм задачи и ответы
Проблема # 1
Найдите x для
журнал 2 ( x ) + журнал 2 ( x -3) = 2
Решение:
Используя правило продукта:
журнал 2 ( x ∙ ( x -3)) = 2
Изменение формы логарифма в соответствии с определением логарифма:
х ∙ ( х -3) = 2 2
Или
х 2 -3 х -4 = 0
Решение квадратного уравнения:
x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1
Поскольку для отрицательных чисел логарифм не определен, ответ будет следующим:
х = 4
Проблема # 2
Найдите x для
журнал 3 ( x +2) - журнал 3 ( x ) = 2
Решение:
Используя правило частного:
журнал 3 (( x +2) / x ) = 2
Изменение формы логарифма в соответствии с определением логарифма:
( х +2) / х = 3 2
Или
х +2 = 9 х
Или
8 х = 2
Или
х = 0,25
График log (x)
log (x) не определен для действительных неположительных значений x:
Таблица логарифмов
| х | журнал 10 x | журнал 2 x | журнал e x |
|---|---|---|---|
| 0 | неопределенный | неопределенный | неопределенный |
| 0 + | - ∞ | - ∞ | - ∞ |
| 0,0001 | -4 | -13,287712 | -9,210340 |
| 0,001 | -3 | -9,965784 | -6,907755 |
| 0,01 | -2 | -6,643856 | -4,605170 |
| 0,1 | -1 | -3,321928 | -2,302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0,301030 | 1 | 0,693147 |
| 3 | 0,477121 | 1,584963 | 1.098612 |
| 4 | 0,602060 | 2 | 1,386294 |
| 5 | 0,698970 | 2,321928 | 1,609438 |
| 6 | 0,778151 | 2,584963 | 1,791759 |
| 7 | 0,845098 | 2,807355 | 1,945910 |
| 8 | 0,903090 | 3 | 2,079442 |
| 9 | 0,954243 | 3,169925 | 2,197225 |
| 10 | 1 | 3,321928 | 2,302585 |
| 20 | 1,301030 | 4,321928 | 2,995732 |
| 30 | 1,477121 | 4,906891 | 3,401197 |
| 40 | 1,602060 | 5,321928 | 3,688879 |
| 50 | 1,698970 | 5,643856 | 3,912023 |
| 60 | 1,778151 | 5,906991 | 4,094345 |
| 70 | 1,845098 | 6,129283 | 4,248495 |
| 80 | 1,903090 | 6,321928 | 4,382027 |
| 90 | 1,954243 | 6,491853 | 4,499810 |
| 100 | 2 | 6,643856 | 4,605170 |
| 200 | 2,301030 | 7,643856 | 5,298317 |
| 300 | 2,477121 | 8,228819 | 5,703782 |
| 400 | 2,602060 | 8,643856 | 5,991465 |
| 500 | 2,698970 | 8,965784 | 6,214608 |
| 600 | 2,778151 | 9,228819 | 6,396930 |
| 700 | 2,845098 | 9,451211 | 6,55 · 1080 |
| 800 | 2,903090 | 9,643856 | 6,684612 |
| 900 | 2,954243 | 9,813781 | 6,802395 |
| 1000 | 3 | 9,965784 | 6,907755 |
| 10000 | 4 | 13,287712 | 9.210340 |
Смотрите также
- Правила логарифмирования
- Изменение логарифма основания
- Логарифм нуля
- Логарифм единицы
- Логарифм бесконечности
- Логарифм отрицательного числа
- Калькулятор логарифмов
- Логарифм график
- Таблица логарифмов
- Калькулятор натурального логарифма
- Натуральный логарифм - ln x
- е постоянная
- Децибел (дБ)
